
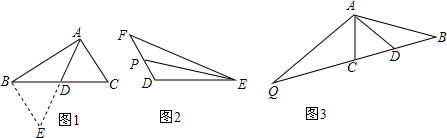
分析 (1)根据全等三角形的判定即可得到结论;
(2)延长EP至点Q,使PQ=PE,连接FQ,根据全等三角形的性质得到FQ=DE=3,根据三角形的三边关系即可得到结论;
(3)延长AD到M,使MD=AD,连接BM,于是得到AM=2AD由已知条件得到BD=CD,根据全等三角形的性质得到BM=CA,∠M=∠CAD,于是得到∠BAC=∠BAM+∠CAD=∠BAM+∠M,推出△ACQ≌△MBA,根据全等三角形的性质即可得到结论.
解答 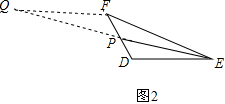 (1)证明:在△ADC与△EDB中,
(1)证明:在△ADC与△EDB中,
$\left\{\begin{array}{l}{AD=DE}\\{∠ADC=∠BDE}\\{CD=BD}\end{array}\right.$,
∴△ADC≌△EDB;
故答案为:△ADC≌△EDB;
(2)解:如图2,延长EP至点Q,使PQ=PE,连接FQ,
在△PDE与△PQF中,
$\left\{\begin{array}{l}{PE=PQ}\\{∠EPD=∠QPF}\\{PD=PF}\end{array}\right.$,
∴△PEP≌△QFP,
∴FQ=DE=3,
在△EFQ中,EF-FQ<QE<EF+FQ,
即5-3<2x<5+3,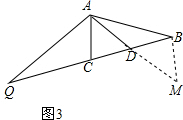
∴x的取值范围是1<x<4;
故答案为:1<x<4;
(3)证明:如图3,延长AD到M,使MD=AD,连接BM,
∴AM=2AD,
∵AD是△ABC的中线,
∴BD=CD,
在△BMD与△CAD中,
$\left\{\begin{array}{l}{MD=AD}\\{∠BDA=∠CDA}\\{BD=CD}\end{array}\right.$,
∴△BMD≌△CAD,
∴BM=CA,∠M=∠CAD,
∴∠BAC=∠BAM+∠CAD=∠BAM+∠M,
∵∠ACB=∠Q+∠CAQ,AB=BC,
∵∠ACQ=180°-(∠Q+∠CAQ),∠MBA=180°-(∠BAM+∠M),
∴∠ACQ=∠MBA,
∵QC=BC,
∴QC=AB,
在△ACQ与△MBA中,
$\left\{\begin{array}{l}{BM=CA}\\{∠ACQ=∠MBA}\\{QC=AB}\end{array}\right.$,
∴△ACQ≌△MBA,
∴AQ=AM=2AD.
点评 本题考查了全等三角形的判定和性质,三角形的中线的定义,三角形的三边关系,正确的作出图形是解题的关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
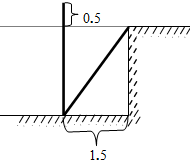 如图,小刚准备测量一条河的深度,他把一根竹竿垂直插到离岸边1.5米远的水底(不计淤泥深度),竹竿高出水面0.5米,再把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐;请推断河水的深度为几米?
如图,小刚准备测量一条河的深度,他把一根竹竿垂直插到离岸边1.5米远的水底(不计淤泥深度),竹竿高出水面0.5米,再把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐;请推断河水的深度为几米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
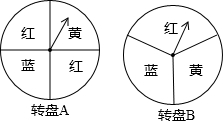 小明和小芳做一个“配色”的游戏,下图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色,这种情况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情况下小明获胜;在其它情况下,则小明、小芳不分胜负.
小明和小芳做一个“配色”的游戏,下图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色,这种情况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情况下小明获胜;在其它情况下,则小明、小芳不分胜负.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com