
【题目】某游客计划测量这座塑像的高度,(如图1),由于游客无法直接到达塑像底部,因此该游客计划借助坡面高度来测量塑像的高度;如图2,在塑像旁山坡坡脚A处测得塑像头顶C的仰角为75°,当从A处沿坡面行走10米到达P处时,测得塑像头顶C的仰角刚好为45°,已知山坡的坡度i=1:3,且O,A,B在同一直线上,求塑像的高度.(侧倾器高度忽略不计,结果精确到0.1米,参考数据:cos75°≈0.3,tan75°≈3.7,![]() ,
,![]() ,
,![]() )
)
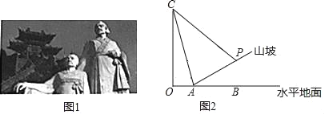
【答案】塑像的高度约为 17.5 米.
【解析】
过点P作PE⊥OB于点E,PF⊥OC于点F,设PE=x,则AE=3x,在Rt△AEP中根据勾股定理得PE,在Rt△AOC中,由tan75°求得m的值,继而可得答案.
过点 P 作 PE⊥OB 交 OB 于点 E,PF⊥OC 交 OC 于点 F,
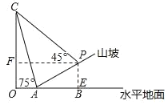
∵i=1:3,AP=10,
设 PE=x,则 AE=3x,
在 Rt△AEP 中,x2+(3x)2=102,
解得:![]() 或
或![]() (舍),
(舍),
∴![]() ,则
,则![]() ,
,
∵∠CPF=∠PCF=45°,
∴CF=PF,
设 CF=PF=m 米,则![]() 米,
米,![]() 米,
米,
在 Rt△AOC 中,![]() 即
即![]()
解得:m≈14.3,
∴![]() 米,
米,
答:塑像的高度约为 17.5 米.


 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】《歌手—当打之年》是湖南卫视最受欢迎的娱乐节目,奇袭挑战赛在每周五晚准时进行,7名主打歌手进行比赛的同时还要接受1名奇袭歌手挑战.近期即将进行终极奇袭战,奇袭歌手艾热将挑战徐佳莹(女)、米希亚(女)、萧敬腾、华晨宇、周深、声入人心男团、旅行团乐队.
(1)当主持人询问艾热准备奇袭哪位歌手时,艾热透露“希望和男性嗓音去比试”,那周深被奇袭的概率是 ;
(2)7名主打歌手比赛的上场顺序是通过抽签方式进行,若已经知道前4位歌手的上场顺序,还有华晨宇、米希亚、周深不知道,那么华晨宇和周深两位是相邻出场的概率是多少.(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化。某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图。请你根据图中提供的信息完成下列问题:
(1)求被调查学生的人数,并将条形统计图补充完整;
(2)求扇形统计图中的A等对应的扇形圆心角的度数;
(3)已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“禹州钧瓷”名扬天下,某网店专门销售某种品牌的钧瓷花瓶,成本为40元/件,每天销量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
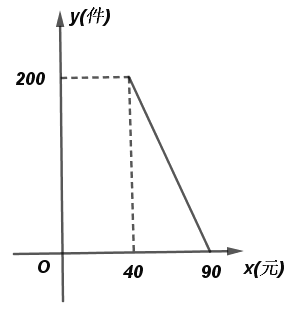
(1)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)如果规定每天钧瓷花瓶的销售量不低于120件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少元?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出100元给希望工程,为了保证捐款后每天剩余利润不低于2000元,试确定该钧瓷花瓶销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c交x轴于A,B两点,交y轴于点C,直线y=x﹣3经过B,C两点.
(1)求抛物线的解析式;
(2)点P是第四象限内抛物线上的动点,过点P作PD⊥x轴于点D,交直线BC于点M,连接AC,过点M作MN⊥AC于点N,设点P的横坐标为t.
①求线段MN的长d与t之间的函数关系式(不要求写出自变量t的取值范围);
②点Q是平面内一点,是否存在一点P,使以B,C,P,Q为顶点的四边形为矩形?若存在,请直接写出t的值;若不存在,请说明理由.
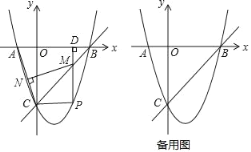
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),则下列说法错误的是( )
A.a+c=0
B.无论a取何值,此二次函数图象与x轴必有两个交点,且函数图象截x轴所得的线段长度必大于2
C.当函数在x<![]() 时,y随x的增大而减小
时,y随x的增大而减小
D.当﹣1<m<n<0时,m+n<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在多项式的乘法公式中,完全平方公式![]() 是其中重要的一个.
是其中重要的一个.
(1)请补全完全平方公式的推导过程:
![]() ,
,
![]() ,
,
![]() .
.
(2)如图,将边长为![]() 的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,请你结合图给出完全平方公式的几何解释.
的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,请你结合图给出完全平方公式的几何解释.
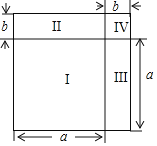
(3)用完全平方公式求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
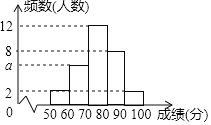
【题目】为了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘成如图所示的频数分布直方图,己知成绩x(单位:分)均满足“50≤x<100”.根据图中信息回答下列问题:
(1)图中a的值为 ;
(2)若要绘制该样本的扇形统计图,则成绩x在“70≤x<80”所对应扇形的圆心角度数为 度;
(3)此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,则获得“优秀“的学生大约有 人:
(4)在这些抽查的样本中,小明的成绩为92分,若从成绩在“50≤x<60”和“90≤x<100”的学生中任选2人,请用列表或画树状图的方法,求小明被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com