
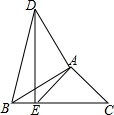
 如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 先利用旋转的性质得AE=AC,AD=AB,∠ADE=∠ABC=30°,∠DAB=∠EAC,再由AE=AC得到∠AEC=∠C=45°,所以∠EAC=90°=∠DAB,接着判断△ADB为等腰直角三角形得到∠ADB=45°,然后计算∠ADB-∠ADE即可.
解答 解:∵△ABC绕点A顺时针旋转后得到△ADE,
∴AE=AC,AD=AB,∠ADE=∠ABC=30°,∠DAB=∠EAC,
∵AE=AC,
∴∠AEC=∠C=45°,
∴∠EAC=90°,
∴∠DAB=90°,
∴△ADB为等腰直角三角形,
∴∠ADB=45°,
∴∠BDE=∠ADB-∠ADE=45°-30°=15°.
故选A.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是证明△ABD为等腰直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
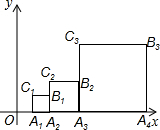 如图,正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn,如图位置依次摆放,已知点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0).
如图,正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn,如图位置依次摆放,已知点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
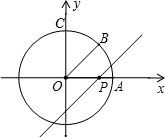 如图,⊙O是以数轴原点O为圆心,半径为3的圆,与坐标轴的正半轴分别交于A、C两点,OB平分∠AOC,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,则线段OP的取值范围是0<OP≤3$\sqrt{2}$.
如图,⊙O是以数轴原点O为圆心,半径为3的圆,与坐标轴的正半轴分别交于A、C两点,OB平分∠AOC,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,则线段OP的取值范围是0<OP≤3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某天,小华到学校时发现有物品遗忘在家中,此时离上课还有15分钟,于是立即步行回家去取.同时,他爸爸从家里出发骑自行车以他3倍的速度给他送遗忘的物品,两人在途中相遇,相遇后小华立即坐爸爸的自行车赶回学校.爸爸和小华在这个过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系如图所示(假设骑自行车和步行的速度始终保持不变).下列说法:
某天,小华到学校时发现有物品遗忘在家中,此时离上课还有15分钟,于是立即步行回家去取.同时,他爸爸从家里出发骑自行车以他3倍的速度给他送遗忘的物品,两人在途中相遇,相遇后小华立即坐爸爸的自行车赶回学校.爸爸和小华在这个过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系如图所示(假设骑自行车和步行的速度始终保持不变).下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com