
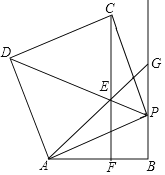
【题目】如图,过线段AB的端点B作射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
(1)求证:![]() ≌
≌![]() ;
;
(2)判断CF与AB的位置关系,并说明理由;
(3)试探究AE+EF+AF与2AB是否相等,并说明理由.
【答案】(1)见解析;(2)CF⊥AB,见解析;(3)AE+EF+AF=2AB,见解析
【解析】
(1)四边形APCD正方形,则DP平分∠APC,PC=PA,∠APD=∠CPD=45°,即可求解;
(2)△AEP≌△CEP,则∠EAP=∠ECP,而∠EAP=∠BAP,则∠BAP=∠FCP,令CF与线段AP交于点M,则∠FCP+∠CMP=90°,则∠AMF+∠PAB=90°即可求解;
(3)证明△PCN≌△APB(AAS),则CN=PB=BF,PN=AB,即可求解.
解:(1)证明:∵四边形APCD正方形,
∴DP平分∠APC,PC=PA,
∴∠APD=∠CPD=45°,
∵PE=PE,
∴△AEP≌△CEP(SAS);
(2)CF⊥AB,理由如下:
∵△AEP≌△CEP,
∴∠EAP=∠ECP,
∵∠EAP=∠BAP,
∴∠BAP=∠FCP,
令CF与线段AP交于点M,
∵∠FCP+∠CMP=90°,∠AMF=∠CMP,
∴∠AMF+∠PAB=90°,
∴∠AFM=90°,
∴CF⊥AB;
(3)过点C作CN⊥PB.
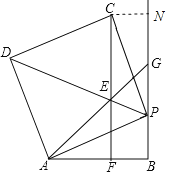
∵CF⊥AB,BG⊥AB,
∴FC∥BN,
∴∠CPN=∠PCF=∠EAP=∠PAB,
又AP=CP,
∴△PCN≌△APB(AAS),
∴CN=PB=BF,PN=AB,
∵△AEP≌△CEP,
∴AE=CE,
∴AE+EF+AF=CE+EF+AF
=BN+AF
=PN+PB+AF
=AB+CN+AF
=AB+BF+AF
=2AB,
即AE+EF+AF=2AB.


科目:初中数学 来源: 题型:
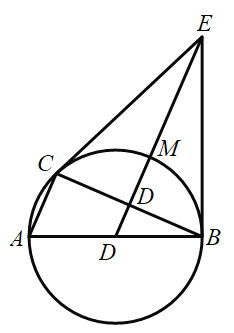
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,点
上,点![]() 为弦
为弦![]() 的中点,射线
的中点,射线![]() 与圆周及切线
与圆周及切线![]() 分别交于点
分别交于点![]() 和点
和点![]() ,连接
,连接![]() .
.
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)若直径![]() ,填空:①连接
,填空:①连接![]() ,当
,当![]() _________
_________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]() ________时,四边形
________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解今年初三学生的数学学习情况,某校在第一轮模拟测试后,对初三全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:
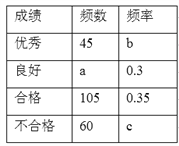
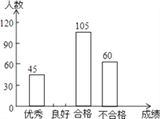
(1)该校初三学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路程如图所示,第一次移动到点A1,第二次移动到点A2,第n次移动到点An,则点A2020的坐标是( )

A.(1010,0)B.(1010,1)C.(1009,0)D.(1009,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解九年级的600名学生每天的自主学习情况,随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两副不完整的统计图(图1图2),请根据统计图中的信息回答下列问题:
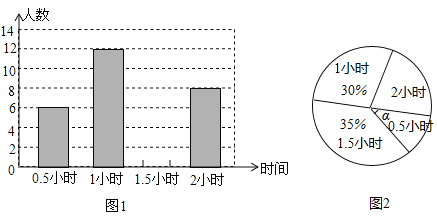
(1)本次调查的学生人数是 人;
(2)图2中角![]() 是 度;
是 度;
(3)将图1条形统计图补充完整;
(4)估算该校九年级学生自主学习不少于1.5小时有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为 1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为( )
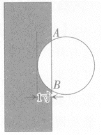
A.13B.24C.26D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.
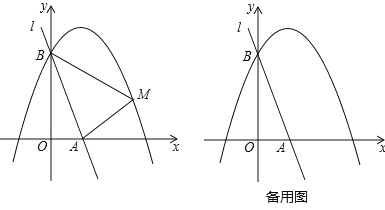
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
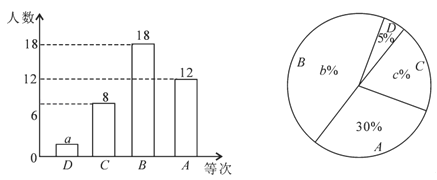
(1)a= ,b= ,c= ;
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为 度;
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com