
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,点
上,点![]() 为弦
为弦![]() 的中点,射线
的中点,射线![]() 与圆周及切线
与圆周及切线![]() 分别交于点
分别交于点![]() 和点
和点![]() ,连接
,连接![]() .
.
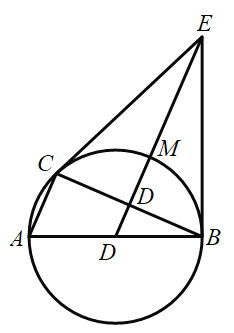
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)若直径![]() ,填空:①连接
,填空:①连接![]() ,当
,当![]() _________
_________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]() ________时,四边形
________时,四边形![]() 是正方形.
是正方形.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
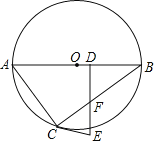
【题目】如图,已知AB是⊙O的直径,C是⊙O上的一点,D是AB上的一点,DE⊥AB于D,DE交BC于F,且EF=EC.
(1)求证:EC是⊙O的切线;
(2)若BD=4,BC=8,圆的半径OB=5,求切线EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() 的边长为4,点
的边长为4,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,当![]() 时,求证:
时,求证:![]() 平分
平分![]() ;
;
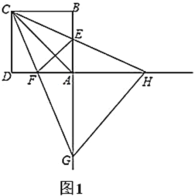
(2)如图2,将图1中的![]() 绕点
绕点![]() 逆时针旋转,其他条件不变,(1)的结论是否成立?说明理由;
逆时针旋转,其他条件不变,(1)的结论是否成立?说明理由;
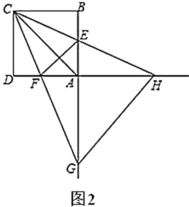
(3)当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克10元.公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中![]() ).
).
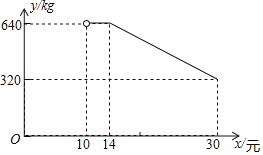
(1)直接写出y与x之间的函数关系式及自变量的取值范围.
(2)若农贸公司每天销售该特产的利润要达到3100元,则销售单价x应定为多少元?
(3)设每天销售该特产的利润为W元,若![]() ,求:销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
,求:销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,若点
,若点![]() 是
是![]() 的中点,则
的中点,则![]() 的周长是( )
的周长是( )
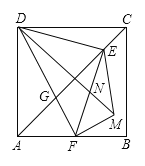
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
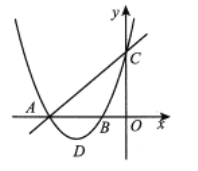
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,经过
,经过![]() ,
,![]() 两点的抛物线
两点的抛物线![]() 与
与![]() 轴的负半轴的另一交点为
轴的负半轴的另一交点为![]() ,且
,且![]()
(1)求该抛物线的解析式及抛物线顶点![]() 的坐标;
的坐标;
(2)点![]() 是射线
是射线![]() 上一点,问是否存在以点
上一点,问是否存在以点![]() ,
,![]() ,
,![]() 为顶点的三角形,与
为顶点的三角形,与![]() 相似,若存在,请求出点
相似,若存在,请求出点![]() 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
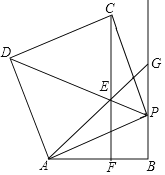
【题目】如图,过线段AB的端点B作射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
(1)求证:![]() ≌
≌![]() ;
;
(2)判断CF与AB的位置关系,并说明理由;
(3)试探究AE+EF+AF与2AB是否相等,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com