
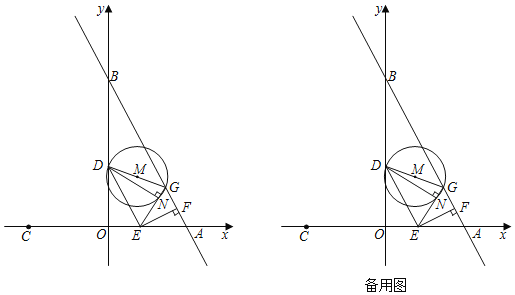
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНЉ2x+6гыxжсЃЌyжсЗжБ№НЛAЃЌBСНЕуЃЌЕуAЙигкдЕуOЕФЖдГЦЕуЪЧЕуCЃЌЖЏЕуEДгAГіЗЂвдУПУы1ИіЕЅЮЛЕФЫйЖШдЫЖЏЕНЕуCЃЌЕуDдкЯпЖЮOBЩЯТњзуtanЁЯDEOЃН2ЃЌЙ§EЕузїEFЁЭABгкЕуFЃЌЕуAЙигкЕуFЕФЖдГЦЕуЮЊЕуGЃЌвдDGЮЊжБОЖзїЁбMЃЌЩшЕуEдЫЖЏЕФЪБМфЮЊtУыЃЛ
ЃЈ1ЃЉЕБЕуEдкЯпЖЮOAЩЯдЫЖЏЃЌtЃНЁЁЁЁЪБЃЌЁїAEFгыЁїEDOЕФЯрЫЦБШЮЊ1ЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБЁбMгыyжсЯрЧаЪБЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉШєжБЯпEGгыЁбMНЛгкЕуNЃЌЪЧЗёДцдкtЪЙNGЃН![]() ЃЌШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃЌШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉtЃН
ЃЛЃЈ2ЃЉtЃН![]() Лђ5ЃЛЃЈ3ЃЉДцдкЃЌtЃН
Лђ5ЃЛЃЈ3ЃЉДцдкЃЌtЃН![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
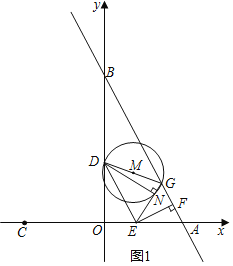
ЃЈ1ЃЉЯШЧѓжБЯпгызјБъжсЕФНЛЕузјБъЃЌдйжЄЁїAEFЁзЁїEDOЁзЁїABOЃЌгЩЁїAEFгыЁїEDOЕФЯрЫЦБШЮЊ1ЃК![]() ЃЌМДПЩЧѓЕУtЕФжЕЃЛ
ЃЌМДПЩЧѓЕУtЕФжЕЃЛ
ЃЈ2ЃЉгЩЁбMгыyжсЯрЧаПЩжЊЃКDGЁЭyжсЃЌЗжСНжжЧщПіЃК0ЁмtЁм3Лђ3ЃМtЁм6ЃЌЗжБ№гЩDЁЂGЕФзнзјБъЯрЕШНЈСЂЗНГЬЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЗжШ§жжЧщПіЃК0ЁмtЁм![]() Лђ
Лђ![]() ЃМtЁм3Лђ3ЃМtЁм6ЃЌЗжБ№НЈСЂЗНГЬЧѓНтМДПЩЃЎ
ЃМtЁм3Лђ3ЃМtЁм6ЃЌЗжБ№НЈСЂЗНГЬЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉдкyЃНЉ2x+6жаЃЌСюxЃН0ЃЌЕУЃКyЃН6ЃЌ
СюyЃН0ЃЌЕУЃКЉ2x+6ЃН0ЃЌ
НтЕУЃКxЃН3ЃЌ
ЁрAЃЈ3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ6ЃЉЃЌCЃЈЉ3ЃЌ0ЃЉ
ЁрOAЃН3ЃЌOBЃН6ЃЌABЃН3![]() ЃЌAEЃНtЃЌOEЃН3ЉtЃЌ
ЃЌAEЃНtЃЌOEЃН3ЉtЃЌ
ЁрtanЁЯBAOЃН![]() ЃН2
ЃН2
ЁпtanЁЯDEOЃН2
ЁрЁЯBAOЃНЁЯDEO
ЁпEFЁЭAB
ЁрЁЯAFEЃНЁЯDOEЃН90Ёу
ЁрЁїAEFЁзЁїEDOЁзЁїABO
![]() ЃЌМД
ЃЌМД![]()
ЁрAFЃН![]() tЃЛ
tЃЛ
ЁпЁїAEFгыЁїEDOЕФЯрЫЦБШЮЊ1ЃК![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМДOEЃН
ЃЌМДOEЃН![]() AF
AF
Ёр3ЉtЃН![]() ЁС
ЁС![]() tЃЌ
tЃЌ
НтЕУЃКtЃН![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃКtЃН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпЁбMгыyжсЯрЧа
ЁрDGЁЭyжс
ЕБ0ЁмtЁм3ЪБЃЌ![]()
ЁпtanЁЯDEOЃН2
Ёр![]()
Ёр![]()
Ёп![]() ЃЌЁїAEFЁзЁїABO
ЃЌЁїAEFЁзЁїABO
Ёр![]()
Ёр![]()
ЁпЕуAЁЂGЙигкЕуFЖдГЦ
Ёр![]()
Ёр![]()
НЋ![]() ДњШы
ДњШы![]() жаЃЌЕУЃЌ
жаЃЌЕУЃЌ![]()
НтЕУ![]() ЃЌ
ЃЌ
ЁрGЃЈ3Љ![]() tЃЌ
tЃЌ![]() tЃЉЃЌDЃЈ0ЃЌ6Љ2tЃЉЃЌ
tЃЉЃЌDЃЈ0ЃЌ6Љ2tЃЉЃЌ
Ёр![]() tЃН6Љ2tЃЌНтЕУЃКtЃН
tЃН6Љ2tЃЌНтЕУЃКtЃН![]() ЃЛ
ЃЛ
ЕБ3ЃМtЁм6ЪБЃЌЭЌРэЕУGЃЈ3Љ![]() tЃЌ
tЃЌ![]() tЃЉЃЌDЃЈ0ЃЌ2tЉ6ЃЉЃЌ
tЃЉЃЌDЃЈ0ЃЌ2tЉ6ЃЉЃЌ
Ёр![]() tЃН2tЉ6ЃЌНтЕУЃКtЃН5ЃЌ
tЃН2tЉ6ЃЌНтЕУЃКtЃН5ЃЌ
злЩЯЫљЪіЃЌЕБЁбMгыyжсЯрЧаЪБЃЌtЃН![]() Лђ5ЃЛ
Лђ5ЃЛ
ЃЈ3ЃЉДцдкЃЎ
ЕБ0ЁмtЁм![]() ЪБЃЌGЃЈ3Љ
ЪБЃЌGЃЈ3Љ![]() tЃЌ
tЃЌ![]() tЃЉЃЌDЃЈ0ЃЌ6Љ2tЃЉЃЌ
tЃЉЃЌDЃЈ0ЃЌ6Љ2tЃЉЃЌ
ЁпЕуAЙигкЕуFЕФЖдГЦЕуЮЊЕуGЃЌEFЁЭAB
ЁрEGЃНEAЃНt
ЁпЁЯOEGЃНЁЯOAB+ЁЯEGAЃН2ЁЯOABЃЌЁЯOEDЃНЁЯOAB
ЁрЁЯGEDЃНЁЯOEDЃНЁЯOAB
ЁпDGЮЊжБОЖ
ЁрЁЯDNGЃНЁЯDNEЃНЁЯDOEЃН90ЁуЃЌDEЃНDE
ЁрЁїDENЁеЁїDEOЃЈAASЃЉ
ЁрENЃНOEЃН3ЉtЃЌNGЃНENЉEGЃН3ЉtЉtЃН3Љ2tЃЌ
Ёр3Љ2tЃН![]() ЃЌ
ЃЌ
НтЕУЃКtЃН![]() ЃЌ
ЃЌ
ЕБ![]() ЃМtЁм3ЪБЃЌNGЃНEGЉENЃНtЉЃЈ3ЉtЃЉЃН2tЉ3
ЃМtЁм3ЪБЃЌNGЃНEGЉENЃНtЉЃЈ3ЉtЃЉЃН2tЉ3
Ёр2tЉ3ЃН![]() ЃЌ
ЃЌ
НтЕУЃКtЃН![]() ЃЛ
ЃЛ
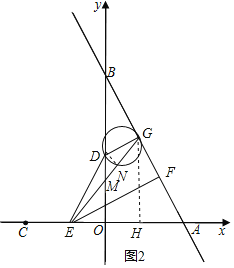
ЕБ3ЃМtЁм6ЪБЃЌШчЭМ2ЃЌСЌНгDNЃЌЙ§GзїGHЁЭxжсгкHЃЌ
ЁпDGЪЧжБОЖЃЌ
ЁрЁЯDNGЃНЁЯDNEЃН90ЁуЃЌ
ЁпЁЯDMNЃНЁЯEMO
ЁрЁїDMNЁзЁїEMO
ЁрЁЯMDNЃНЁЯOEM
ЁпGHЁЮyжс
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
гЩЃЈ2ЃЉЕУ![]() ЃЌ
ЃЌ
Ёп![]() жсЃЌ
жсЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр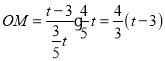 ЃЌ
ЃЌ
ЁрDMЃНODЉOMЃН2ЃЈtЉ3ЃЉЉ![]() ЃЈtЉ3ЃЉЃН
ЃЈtЉ3ЃЉЃН![]() ЃЈtЉ3ЃЉ
ЃЈtЉ3ЃЉ
ЁпtanЁЯOEMЃН![]()
ЁрEMЃН![]() OEЃН
OEЃН![]() ЃЈtЉ3ЃЉЃЌ
ЃЈtЉ3ЃЉЃЌ
ЁрsinЁЯOEMЃН![]() ЃН
ЃН![]() ЃНsinЁЯMDNЃН
ЃНsinЁЯMDNЃН![]()
ЁрMNЃН![]() ЁС
ЁС![]() ЃЈtЉ3ЃЉЃН
ЃЈtЉ3ЃЉЃН![]() ЃЈtЉ3ЃЉ
ЃЈtЉ3ЃЉ
ЁрNGЃНEGЉEMЉMNЃНtЉ![]() ЃЈtЉ3ЃЉЉ
ЃЈtЉ3ЃЉЉ![]() ЃЈtЉ3ЃЉЃН
ЃЈtЉ3ЃЉЃН![]() Љ
Љ![]() tЃЌ
tЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃКtЃН![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃЌtЃН![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮABCDЕФЖЅЕуAдкyжсЩЯЃЌЕуBЁЂCдкxжсЩЯЃЛOAЁЂOBГЄЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬx2Љ7x+12ЃН0ЕФСНИіИљЃЌЧвOAЃОOBЃЌBCЃН6ЃЛ
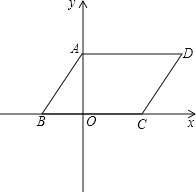
ЃЈ1ЃЉаДГіЕуDЕФзјБъЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєЕуEЮЊxжсЩЯвЛЕуЃЌЧвSЁїAOEЃН![]() ЃЌ
ЃЌ
ЂйЧѓЕуEЕФзјБъЃЛ
ЂкХаЖЯЁїAOEгыЁїAODЪЧЗёЯрЫЦВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуMЪЧзјБъЯЕФквЛЕуЃЌдкжБЯпABЩЯЪЧЗёДцдкЕуFЃЌЪЙвдAЁЂCЁЂFЁЂMЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃПШєДцдкЃЌЧыжБНгаДГіFЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуOЮЊ![]() аББпABЩЯЕФвЛЕуЃЌвдOAЮЊАыОЖЕФ
аББпABЩЯЕФвЛЕуЃЌвдOAЮЊАыОЖЕФ![]() гыBCЧагкЕуDЃЌгыACНЛгкЕуEЃЌСЌНгAD.
гыBCЧагкЕуDЃЌгыACНЛгкЕуEЃЌСЌНгAD.
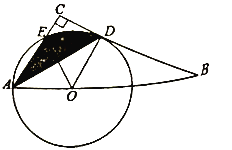
ЃЈ1ЃЉЧѓжЄЃКADЦНЗж![]()
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓвѕгАВПЗжЕФУцЛ§.ЃЈНсЙћБЃСє
ЃЌЧѓвѕгАВПЗжЕФУцЛ§.ЃЈНсЙћБЃСє![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
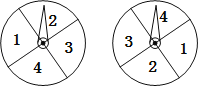
ЁОЬтФПЁПбЇЩњМзгыбЇЩњввЭцвЛжжзЊХЬгЮЯЗЃЎШчЭМЪЧСНИіЭъШЋЯрЭЌЕФзЊХЬЃЌУПИізЊХЬБЛЗжГЩУцЛ§ЯрЕШЕФЫФИіЧјгђЃЌЗжБ№гУЪ§зжЁА1ЁБЁЂЁА2ЁБЁЂЁА3ЁБЁЂЁА4ЁББэЪОЃЎЙЬЖЈжИеыЃЌЭЌЪБзЊЖЏСНИізЊХЬЃЌШЮЦфздгЩЭЃжЙЃЌШєСНжИеыЫљжИЪ§зжЕФЛ§ЮЊЦцЪ§ЃЌдђМзЛёЪЄЃЛШєСНжИеыЫљжИЪ§зжЕФЛ§ЮЊХМЪ§ЃЌдђввЛёЪЄЃЛШєжИеыжИЯђЩШаЮЕФЗжНчЯпЃЌдђЖМжизЊвЛДЮЃЎдкИУгЮЯЗжаввЛёЪЄЕФИХТЪЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
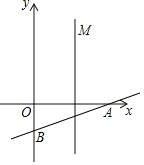
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃН![]() xЉ2гыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂBЃЌЙ§ЕуCЃЈ2ЃЌЉ1ЃЉзїжБЯпlЁЮyжсЃЌЕуMЮЊжБЯпlЩЯЕФвЛИіЖЏЕуЃЌвдЕуMЮЊдВаФЃЌMOЮЊАыОЖзїдВЃЌЕБЁбMгыжБЯпABЯрЧаЪБЃЌЕуMЕФзјБъЮЊ_____ЃЎ
xЉ2гыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂBЃЌЙ§ЕуCЃЈ2ЃЌЉ1ЃЉзїжБЯпlЁЮyжсЃЌЕуMЮЊжБЯпlЩЯЕФвЛИіЖЏЕуЃЌвдЕуMЮЊдВаФЃЌMOЮЊАыОЖзїдВЃЌЕБЁбMгыжБЯпABЯрЧаЪБЃЌЕуMЕФзјБъЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаЙњЙХДњЫуЪщЁЖЫуЗЈЭГзкЁЗжагаетбљвЛЕРЬтЃКМзИЯШКбђж№ВнУЏЃЌввзЇЗЪбђЫцЦфКѓЃЌЯЗЮЪМзМАвЛАйЗёЃПМздЦЫљЫЕЮоВюУ§ЃЌШєЕУетАувЛШКДеЃЌдйЬэАыШКаЁАыЃЈзЂЃКЫФЗжжЎвЛЕФвтЫМЃЉШКЃЌЕУФувЛжЛРДЗНДеЃЌаўЛњАТУюЫВЮЭИЃПДѓвтЪЧЫЕЃКФСбђШЫИЯзХвЛШКбђШЅбАевВнГЄЕУУЏЪЂЕФЕиЗНЗХФСЃЌгавЛИіЙ§ТЗШЫЧЃзХ1жЛЗЪбђДгКѓУцИњСЫЩЯРДЃЌЫћЖдФСбђШЫЫЕФуИЯЕФетШКбђДѓИХга100жЛАЩЃПФСбђШЫД№ЕРЃКШчЙћетвЛШКбђМгЩЯ1БЖЃЌдйМгЩЯдРДбђШКЕФвЛАыЃЌгжМгЩЯдРДетШКбђЕФЫФЗжжЎвЛЃЌСЌФуЧЃзХЕФетжЛЗЪбђвВЫуНјШЅЃЌВХИеКУТњ100жЛФужЊЕРФСбђШЫЗХФСЕФетШКбђвЛЙВгаЖрЩйжЛТ№ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
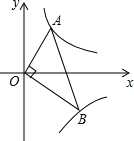
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЁЂBЗжБ№дкЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЃЌyЃНЉ
ЃЈxЃО0ЃЉЃЌyЃНЉ![]() ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌЧвOAЁЭOBЃЌдђ
ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌЧвOAЁЭOBЃЌдђ![]() ЕФжЕЮЊ_____ЃЎ
ЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
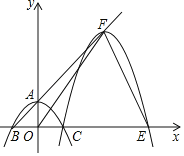
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+cЃЈaЁй0ЃЉгыyжсНЛгкЕуAЃЌгыxжсНЛгкBЃЌCСНЕуЃЈЕуCдкxжсе§АыжсЩЯЃЉЃЌЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌЧвУцЛ§ЮЊ4ЃЌЯжНЋХзЮяЯпбиBAЗНЯђЦНвЦЃЌЦНвЦКѓЕФХзЮяЯпЙ§ЕуCЪБЃЌгыxжсЕФСэвЛНЛЕуЮЊEЃЌЦфЖЅЕуЮЊFЃЎ
ЃЈ1ЃЉЧѓaЁЂcЕФжЕЃЛ
ЃЈ2ЃЉСЌНгOFЃЌЪдХаЖЯЁїOEFЪЧЗёЮЊЕШбќШ§НЧаЮЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБНЧЁїABCжаЃЌЁЯBAC=90ЁуЃЌDдкBCЩЯЃЌСЌНгADЃЌзїBFЁЭADЗжБ№НЛADгкEЃЌНЛACгкFЃЎ
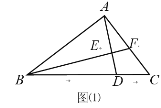
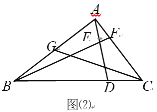
ЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌШєBD=BAЃЌЧѓжЄЃКЁЯBAD=ЁЯC+ЁЯCADЃЛ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌШє BD=4DCЃЌШЁAB ЕФжаЕуGЃЌСЌНгCGНЛADгкMЃЌЧѓжЄЃКЂйGM=2MCЃЛЂк![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com