
【题目】如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,交AC于F.
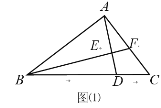
(1)如图(1),若BD=BA,求证:∠BAD=∠C+∠CAD;
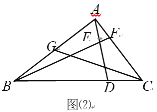
(2)如图(2),若 BD=4DC,取AB 的中点G,连接CG交AD于M,求证:①GM=2MC;②![]() .
.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
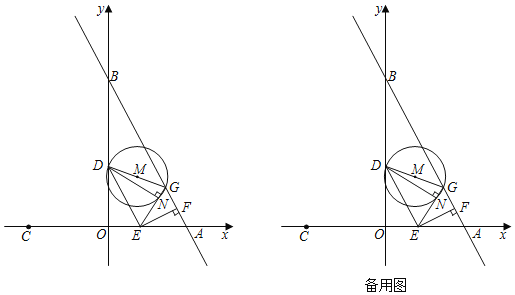
【题目】如图,直线y=﹣2x+6与x轴,y轴分别交A,B两点,点A关于原点O的对称点是点C,动点E从A出发以每秒1个单位的速度运动到点C,点D在线段OB上满足tan∠DEO=2,过E点作EF⊥AB于点F,点A关于点F的对称点为点G,以DG为直径作⊙M,设点E运动的时间为t秒;
(1)当点E在线段OA上运动,t= 时,△AEF与△EDO的相似比为1:![]() ;
;
(2)当⊙M与y轴相切时,求t的值;
(3)若直线EG与⊙M交于点N,是否存在t使NG=![]() ,若存在,求出t的值;若不存在,说明理由.
,若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件![]() 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
![]() 求一次函数
求一次函数![]() 的表达式;
的表达式;
![]() 若该商场获得利润为
若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,点E,F分别是边BC上两点,且![]() .将
.将![]() 绕点O逆时针旋转,当点F与点C重合时,停止旋转.已知,BC=6,设BE=x,EF=y.
绕点O逆时针旋转,当点F与点C重合时,停止旋转.已知,BC=6,设BE=x,EF=y.
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值;
x | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
y | 3 | 2.77 | 2.50 | 2.55 | 2.65 |
(说明:补全表格时相关数值保留一位小数)
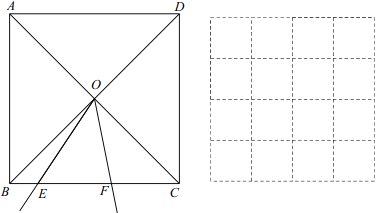
(2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合函数图象,解决问题:当EF=2BE时,BE的长度约为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,半径为2cm的P的圆心在射线OA上,且与点O的距离为6cm,如果P以1cm/s的速度沿直线AB由A向B的方向移动,那么P与直线CD相切时☉P运动的时间是( )
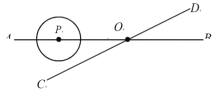
A.3秒或10秒B.3秒或8秒C.2秒或8秒D.2秒或10秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】口袋中有![]() 只乒乓球,其中
只乒乓球,其中![]() 只是红球,另
只是红球,另![]() 只是黄球,它们的大小都一样,现从中任意摸出
只是黄球,它们的大小都一样,现从中任意摸出![]() 只球,
只球,
(1)恰为一红一黄的概率是多少?
(2)两只均为红球的概率是多少?
(3)两只均为黄球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
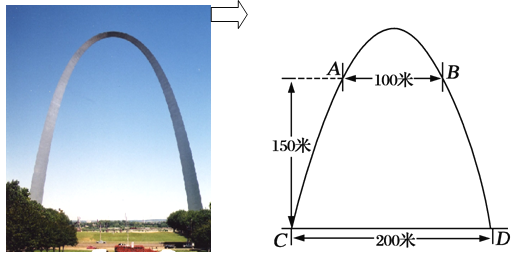
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,等边△ABC中D点为AB边上一动点,E为直线AC上一点,将△ADE沿着DE折叠,点A落在直线BC上,对应点为F,若AB=4,BF:FC=1:3,则线段AE的长度为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com