
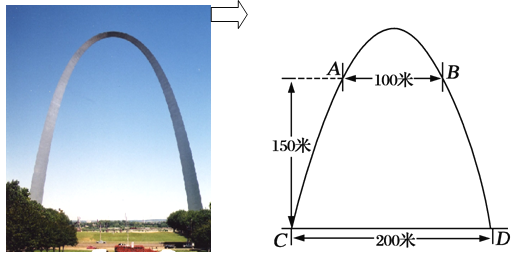
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
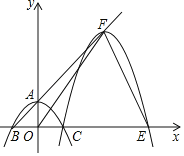
【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一交点为E,其顶点为F.
(1)求a、c的值;
(2)连接OF,试判断△OEF是否为等腰三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,交AC于F.
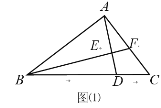
(1)如图(1),若BD=BA,求证:∠BAD=∠C+∠CAD;
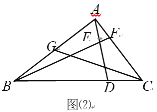
(2)如图(2),若 BD=4DC,取AB 的中点G,连接CG交AD于M,求证:①GM=2MC;②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡居民节约用水,规定每三口之家每月用水量不得超过20吨,超过部分需加价收费.已知小丽家有三口人,今年4月份用水24吨,交水费46元;5月份用水29吨,交水费58.5元.你能知道该市在限定量以内的水费每吨多少元,超过部分的水费每吨多少元吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
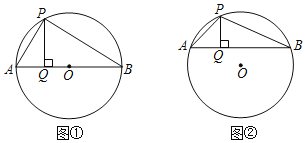
【题目】(1)如图①,AB为⊙O的直径,点P在⊙O上,过点P作PQ⊥AB,垂足为点Q.说明△APQ∽△ABP;
(2)如图②,⊙O的半径为7,点P在⊙O上,点Q在⊙O内,且PQ=4,过点Q作PQ的垂线交⊙O于点A、B.设PA=x,PB=y,求y与x的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com