
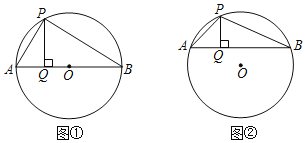
【题目】(1)如图①,AB为⊙O的直径,点P在⊙O上,过点P作PQ⊥AB,垂足为点Q.说明△APQ∽△ABP;
(2)如图②,⊙O的半径为7,点P在⊙O上,点Q在⊙O内,且PQ=4,过点Q作PQ的垂线交⊙O于点A、B.设PA=x,PB=y,求y与x的函数表达式.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据圆周角定理可证∠APB=90°,再根据相似三角形的判定方法:两角对应相等,两个三角形相似即可求证结论;
(2)连接PO,并延长PO交⊙O于点C,连接AC,根据圆周角定理可得∠PAC=90°,∠C=∠B,求得∠PAC=∠PQB,根据相似三角形的性质即可得到结论.
(1)如图①所示:
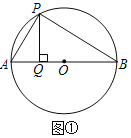
∵AB为⊙O的直径
∴∠APB=90°
又∵PQ⊥AB
∴∠AQP=90°
∴∠AQP=∠APB
又∵∠PAQ=∠BAP
∴△APQ∽△ABP.
(2)如图②,连接PO,并延长PO交⊙O于点C,连接AC.
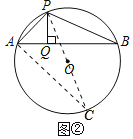
∵PC为⊙O的直径
∴∠PAC=90°
又∵PQ⊥AB
∴∠PQB=90°
∴∠PAC=∠PQB
又∵∠C=∠B(同弧所对的圆周角相等)
∴△PAC∽△PQB
∴![]()
又∵⊙O的半径为7,即PC=14,且PQ=4,PA=x,PB=y
∴![]()
∴![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件![]() 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
![]() 求一次函数
求一次函数![]() 的表达式;
的表达式;
![]() 若该商场获得利润为
若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】口袋中有![]() 只乒乓球,其中
只乒乓球,其中![]() 只是红球,另
只是红球,另![]() 只是黄球,它们的大小都一样,现从中任意摸出
只是黄球,它们的大小都一样,现从中任意摸出![]() 只球,
只球,
(1)恰为一红一黄的概率是多少?
(2)两只均为红球的概率是多少?
(3)两只均为黄球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
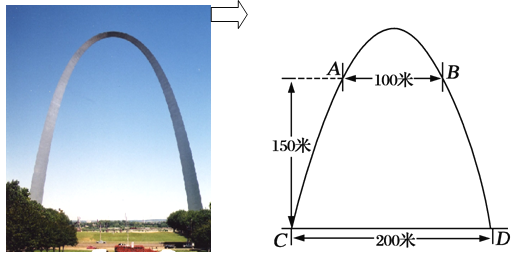
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
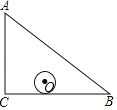
【题目】如图,在△ABC中,AC:BC:AB=3:4:5,⊙O沿着△ABC的内部边缘滚动一圈,若⊙O的半径为1,且圆心O运动的路径长为18,则△ABC的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
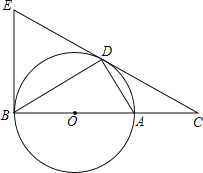
(1)求证:CD2=CACB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
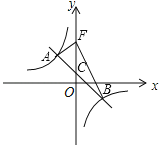
【题目】在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=![]() (k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(1)求一次函数和反比例函数的解析式;
(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,等边△ABC中D点为AB边上一动点,E为直线AC上一点,将△ADE沿着DE折叠,点A落在直线BC上,对应点为F,若AB=4,BF:FC=1:3,则线段AE的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
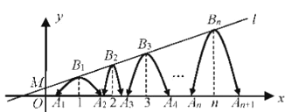
【题目】定义:若抛物线的顶点与![]() 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.如图,直线
轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.如图,直线![]() :
:![]() 经过点
经过点![]() 一组抛物线的顶点
一组抛物线的顶点![]() ,
,![]() ,
,![]() ,…
,…![]() (
(![]() 为正整数),依次是直线
为正整数),依次是直线![]() 上的点,这组抛物线与
上的点,这组抛物线与![]() 轴正半轴的交点依次是:
轴正半轴的交点依次是:![]() ,
,![]() ,
,![]() ,…
,…![]() (
(![]() 为正整数).若
为正整数).若![]() ,当
,当![]() 为( )时,这组抛物线中存在美丽抛物线.
为( )时,这组抛物线中存在美丽抛物线.
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com