
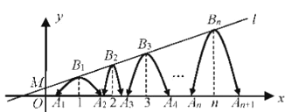
【题目】定义:若抛物线的顶点与![]() 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.如图,直线
轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.如图,直线![]() :
:![]() 经过点
经过点![]() 一组抛物线的顶点
一组抛物线的顶点![]() ,
,![]() ,
,![]() ,…
,…![]() (
(![]() 为正整数),依次是直线
为正整数),依次是直线![]() 上的点,这组抛物线与
上的点,这组抛物线与![]() 轴正半轴的交点依次是:
轴正半轴的交点依次是:![]() ,
,![]() ,
,![]() ,…
,…![]() (
(![]() 为正整数).若
为正整数).若![]() ,当
,当![]() 为( )时,这组抛物线中存在美丽抛物线.
为( )时,这组抛物线中存在美丽抛物线.
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]()
【答案】B
【解析】
由抛物线的对称性可知,所有构成的直角三角形必是以抛物线顶点为直角顶点的等腰三角形,所以此等腰三角形斜边上的高等于斜边的一半,又0<d<1,所以等腰直角三角形斜边的长小于2,所以等腰直角三角形斜边的高一定小于1,即抛物线的顶点纵坐标必定小于1,据此对上一步结论分析可得满足美丽抛物线对应的顶点,再确定抛物线与x轴的交点值与对称轴的距离,从而可求得d的值
解: 直线l:![]() 经过点M(0,
经过点M(0,![]() )则b=
)则b=![]() ,
,
∴直线l:![]()
由抛物线的对称性知:
抛物线的顶点与x轴的两个交点构成的直角三角形必为等腰直角三角形;
∴该等腰三角形的高等于斜边的一半
∵0<d<1
∴该等腰直角三角形的斜边长小于2,斜边上的高小于1(即抛物线的顶点纵坐标小于1)∵当x=1时,![]() <1;
<1;
当x=2时,![]() <1;
<1;
当x=3时,![]() >1;
>1;
∴美丽抛物线的顶点只有![]()
①若![]() 为顶点,由
为顶点,由![]() ,则
,则![]() ,
,
②若![]() 为顶点,由
为顶点,由![]() ,则
,则![]()
综上所述,d的值为![]() 或
或![]() 时,存在美丽抛物线.
时,存在美丽抛物线.
故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
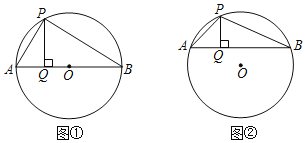
【题目】(1)如图①,AB为⊙O的直径,点P在⊙O上,过点P作PQ⊥AB,垂足为点Q.说明△APQ∽△ABP;
(2)如图②,⊙O的半径为7,点P在⊙O上,点Q在⊙O内,且PQ=4,过点Q作PQ的垂线交⊙O于点A、B.设PA=x,PB=y,求y与x的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
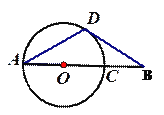
【题目】如图,AD是⊙O的弦,AC是⊙O直径,⊙O的切线BD交AC的延长线于点B,切点为D,∠DAC=30°.
(1)求证:△ADB是等腰三角形;
(2)若BC= ![]() ,则AD的长为 .
,则AD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
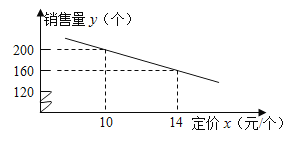
【题目】丹尼斯超市进了一批成本为 8 元/个的文具盒. 调查发现:这种文具盒每个星期的销售量y(个)与它的定价 x(元/个)的关系如图所示:
(1)求这种文具盒每个星期的销售量 y(个)与它的定价 x(元/个)之间的函数关系式(不必写出自变量 x的取值范围);
(2)每个文具盒的定价是多少元,超市每星期销售这种文具盒 (不考虑其他因素)可或得的利润为 1200 元?
(3)若该超市每星期销售这种文具盒的销售量小于 115 个, 且单件利润不低于 4 元(x 为整数),当每个文具盒定价多少 元时,超市每星期利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:![]() 与x轴交于点
与x轴交于点![]() ,与y轴交于点B,点C是线段OA上一动点
,与y轴交于点B,点C是线段OA上一动点![]() 以点A为圆心,AC长为半径作
以点A为圆心,AC长为半径作![]() 交x轴于另一点D,交线段AB于点E,连结OE并延长交
交x轴于另一点D,交线段AB于点E,连结OE并延长交![]() 于点F.
于点F.
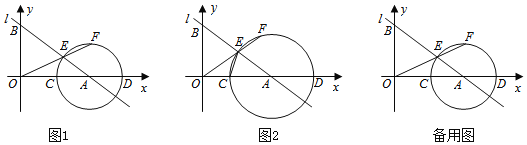
![]() 求直线l的函数表达式和
求直线l的函数表达式和![]() 的值;
的值;
![]() 如图2,连结CE,当
如图2,连结CE,当![]() 时,
时,
![]() 求证:
求证:![]() ∽
∽![]() ;
;
![]() 求点E的坐标;
求点E的坐标;
![]() 当点C在线段OA上运动时,求
当点C在线段OA上运动时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
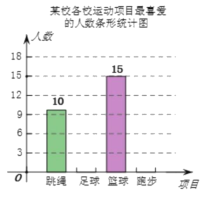
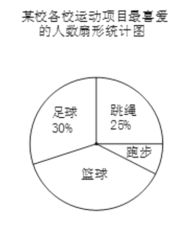
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)在扇形统计图中,“篮球”部分所对应的圆心角度数为__ ;
(4)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是![]() 的直径,点P在BA的延长线上,PD切
的直径,点P在BA的延长线上,PD切![]() 于点D,过点B作
于点D,过点B作![]() ,交PD的延长线于点C,连接AD并延长,交BE于点E.
,交PD的延长线于点C,连接AD并延长,交BE于点E.
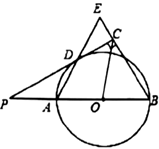
(Ⅰ)求证:AB=BE;
(Ⅱ)连结OC,如果PD=2![]() ,∠ABC=60°,求OC的长.
,∠ABC=60°,求OC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com