
【题目】如图,![]() 为
为![]() 的外接圆,
的外接圆,![]() 为
为![]() 与
与![]() 的交点,
的交点,![]() 为线段
为线段![]() 延长线上一点,且
延长线上一点,且![]() .
.
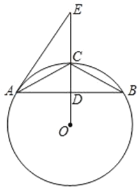
(1)求证:直线![]() 是
是![]() 的切线.
的切线.
(2)若![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .
.
①求![]() 的半径;
的半径;
②求![]() 的内心到点
的内心到点![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)①![]() ;②5.
;②5.
【解析】
(1)连接AO,并延长AO交⊙O于点F,连接CF,由圆周角定理的推论可得∠ACF=90°,可得∠F+∠FAC=90°,由∠EAC=∠ABC,可得∠EAC+∠FAC=90°,即可完成证明;
(2)①由垂径定理可得OD⊥AB,AD=BD=8,由勾股定理可求⊙O的半径;
②作∠CAB的平分线交CD于点H,连接BH,过点H作HM⊥AC,HN⊥BC,则点H是△ABC的内心,由三角形内心的性质可得HM=HN=HD,由三角形的面积公式可求HD的值,即可完成解答.
(1)证明:如图:连接AO,并延长AO交⊙O于点F,连接CF,
∵AF是直径,
∴∠ACF=90°,
∴∠F+∠FAC=90°,
∵∠F=∠ABC,∠ABC=∠EAC,
∴∠EAC=∠F,
∴∠EAC+∠FAC=90°,
∴∠EAF=90°,
∵AO是半径,
∴直线AE是⊙O的切线;

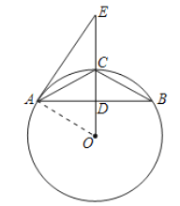
(2)①如图,连接AO,
∵D为AB的中点,OD过圆心,
∴OD⊥AB,AD=BD=![]() AB=8,
AB=8,
∵AO2=AD2+DO2,
∴AO2=82+(AO-6)2,
∴AO=![]() ,
,
∴⊙O的半径为![]() ;
;
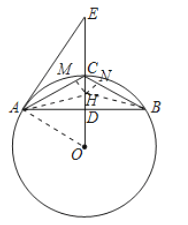
②如图,作∠CAB的平分线交CD于点H,连接BH,过点H作HM⊥AC,HN⊥BC,
∵OD⊥AB,AD=BD,
∴AC=BC,
∴CD平分∠ACB,即点H是△ABC的内心,
∴MH=NH=DH,
在Rt△ACD中,![]() ,
,
∵S△ABC=S△ACH+S△ABH+S△BCH,
∴![]() ×16×6=
×16×6=![]() ×10×MH+
×10×MH+![]() ×16×DH+
×16×DH+![]() ×10×NH,
×10×NH,
∴DH=![]() ,
,
∵OH=CO-CH=CO-( CD-DH),
∴![]() .
.


科目:初中数学 来源: 题型:
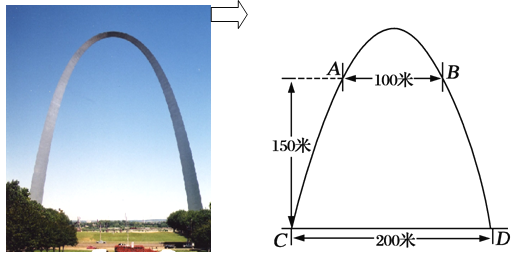
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,等边△ABC中D点为AB边上一动点,E为直线AC上一点,将△ADE沿着DE折叠,点A落在直线BC上,对应点为F,若AB=4,BF:FC=1:3,则线段AE的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C.D是二次函数图象上的一对对称点,一次函数的图象过点B,D.
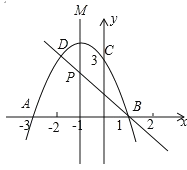
(1)D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
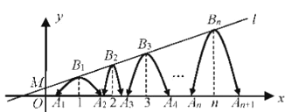
【题目】定义:若抛物线的顶点与![]() 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.如图,直线
轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.如图,直线![]() :
:![]() 经过点
经过点![]() 一组抛物线的顶点
一组抛物线的顶点![]() ,
,![]() ,
,![]() ,…
,…![]() (
(![]() 为正整数),依次是直线
为正整数),依次是直线![]() 上的点,这组抛物线与
上的点,这组抛物线与![]() 轴正半轴的交点依次是:
轴正半轴的交点依次是:![]() ,
,![]() ,
,![]() ,…
,…![]() (
(![]() 为正整数).若
为正整数).若![]() ,当
,当![]() 为( )时,这组抛物线中存在美丽抛物线.
为( )时,这组抛物线中存在美丽抛物线.
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开设“慈善基金”活动以来,受到同学们的广泛帮助,学校为了解全校学生捐款的情况,随机调查了部分学生的捐款金额,并制成如图不完整的统计图表.
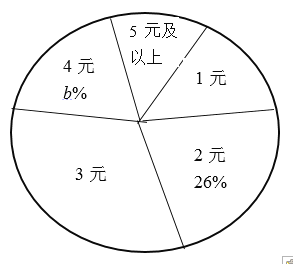
捐款金额 | 1元 | 2元 | 3元 | 4元 | 5元及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)该调查统计数据的中位数是 ,众数是 ;
(3)请计算扇形统计图中的3元所对应的圆心角的度数;
(4)若该校共有2000名学生,根据调查结果,统计该校学生在5元及以上的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com