
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЮЊОиаЮЃЌABЃН4cmЃЌADЃН3cmЃЌЖЏЕуMЁЂNЗжБ№ДгDЁЂBЭЌЪБГіЗЂЃЌЖМвд1cm/УыЕФЫйЖШдЫЖЏЃЌЕуMбиDAЯђЕужеЕуAдЫЖЏЃЌЕуNбиBCЯђжеЕуCдЫЖЏЃЎЙ§ЕуNзїNPЁЭBCЃЌНЛACгкЕуPЃЌСЌНгMPЃЌвбжЊдЫЖЏЕФЪБМфЮЊtУыЃЈ0ЃМtЃМ3ЃЉЃЎ
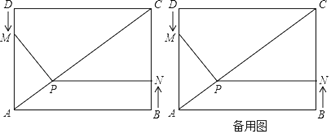
ЃЈ1ЃЉЕБtЃН1УыЪБЃЌЧѓГіPNЕФГЄЃЛ
ЃЈ2ЃЉШєЫФБпаЮCDMPЕФУцЛ§ЮЊsЃЌЪдЧѓsгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉдкдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГвЛЪБПЬtЪЙЫФБпаЮCDMPЕФУцЛ§гыЫФБпаЮABCDЕФУцЛ§БШЮЊ3ЃК8ЃЌШєДцдкЃЌЧыЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ4ЃЉдкЕуMЁЂNдЫЖЏЙ§ГЬжаЃЌЁїMPAФмЗёГЩЮЊвЛИіЕШбќШ§НЧаЮЃПШєФмЃЌЪдЧѓГіЫљгаtЕФПЩФмжЕЃЛШєВЛФмЃЌЪдЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉДцдкЃЌ
ЃЛЃЈ3ЃЉДцдкЃЌ![]() ЃЛЃЈ4ЃЉФмЃЌЕБtЃН1ЛђtЃН
ЃЛЃЈ4ЃЉФмЃЌЕБtЃН1ЛђtЃН![]() ЛђtЃН
ЛђtЃН![]() ЪБЃЌЁїMPAЪЧЕШбќШ§НЧаЮ.
ЪБЃЌЁїMPAЪЧЕШбќШ§НЧаЮ.
ЁОНтЮіЁП
(1)гЩtЃН1жЊBNЃН1ЁЂCNЃНBCЉBNЃН2ЃЌжЄЁїPNCЁзЁїABCЕУ![]() ЃЌОнДЫПЩЕУД№АИЃЛ
ЃЌОнДЫПЩЕУД№АИЃЛ
(2)бгГЄNPНЛADгкЕуQЃЌдђPQЁЭADЃЌгЩЁїPNCЁзЁїABCЕУ![]() ЃЌОнДЫЕУГіPNЃН4Љ
ЃЌОнДЫЕУГіPNЃН4Љ![]() tЁЂPQЃН
tЁЂPQЃН![]() tЃЌИљОнSЫФБпаЮCDMPЃНSЁїACDЉSЁїAMPПЩЕУЃЛ
tЃЌИљОнSЫФБпаЮCDMPЃНSЁїACDЉSЁїAMPПЩЕУЃЛ
(3)ЧѓГіОиаЮABCDЕФУцЛ§ЃЌШЛКѓгЩЬтвтПЩЕУЙигкtЕФЗНГЬЃЌНтЗНГЬМДПЩЧѓЕУД№АИЃЛ
(4)БОЬтвЊЗжШ§жжЧщПіЃКЂйMPЃНPAЃЌФЧУДAQЃНBNЃН![]() AMЃЌПЩгУxЗжБ№БэЪОГіBNКЭAMЕФГЄЃЌШЛКѓИљОнЩЯЪіЕШСПЙиЯЕПЩЧѓЕУxЕФжЕЃЎЂкMAЃНMPЃЌдкжБНЧШ§НЧаЮMQPжаЃЌMQЃНMAЉBNЃЌPQЃНABЉPNИљОнЙДЙЩЖЈРэМДПЩЧѓГіxЕФжЕЃЎЂлMAЃНPAЃЌВЛФбЕУГіAPЃН
AMЃЌПЩгУxЗжБ№БэЪОГіBNКЭAMЕФГЄЃЌШЛКѓИљОнЩЯЪіЕШСПЙиЯЕПЩЧѓЕУxЕФжЕЃЎЂкMAЃНMPЃЌдкжБНЧШ§НЧаЮMQPжаЃЌMQЃНMAЉBNЃЌPQЃНABЉPNИљОнЙДЙЩЖЈРэМДПЩЧѓГіxЕФжЕЃЎЂлMAЃНPAЃЌВЛФбЕУГіAPЃН![]() BNЃЌШЛКѓгУxБэЪОГіAMЕФГЄЃЌМДПЩЧѓГіxЕФжЕЃЎ
BNЃЌШЛКѓгУxБэЪОГіAMЕФГЄЃЌМДПЩЧѓГіxЕФжЕЃЎ
(1)ЕБtЃН1ЪБЃЌBNЃН1ЁЂCNЃНBCЉBNЃН2ЃЌ
ЁпPNЁЭBCЃЌ
ЁрЁЯPNCЃНЁЯBЃН90ЁуЃЌ
ЁрPNЁЮABЃЌ
ЁрЁїPNCЁзЁїABCЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЁрPNЃН![]() ЃЛ
ЃЛ
(2)ШчЭМЃЌбгГЄNPНЛADгкЕуQЃЌдђPQЁЭADЃЌ

гЩЬтвтжЊЃЌDMЃНBNЃНtЃЌAMЃНCNЃН3ЉtЃЌ
ЁпPNЁЮABЃЌ
ЁрЁїPNCЁзЁїABCЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃКPNЃН![]() (3Љt)ЃН4Љ
(3Љt)ЃН4Љ![]() tЃЌ
tЃЌ
ЁпPQЁЭADЃЌ
ЁрЁЯQABЃНЁЯBЃНЁЯNQAЃН90ЁуЃЌ
ЁрЫФБпаЮABNQЪЧОиаЮЃЌ
дђABЃНQNЃН4ЃЌ
ЁрPQЃНQNЉPNЃН4Љ(4Љ![]() t)ЃН
t)ЃН![]() tЃЌ
tЃЌ
ЁрЫФБпаЮCDMPЕФУцЛ§sЃН![]() ЁС3ЁС4Љ
ЁС3ЁС4Љ![]() ЁС(3Љt)ЁС
ЁС(3Љt)ЁС![]() tЃН
tЃН![]() t2Љ2t+6ЃЛ
t2Љ2t+6ЃЛ
(3)ЁпSОиаЮABCDЃН3ЁС4ЃН12ЃЌ
Ёр ЃЌ
ЃЌ
НтЕУЃКtЃН![]() ЃЌ
ЃЌ
ЫљвдtЃН![]() ЪБЫФБпаЮCDMPЕФУцЛ§гыЫФБпаЮABCDЕФУцЛ§БШЮЊ3ЃК8ЃЛ
ЪБЫФБпаЮCDMPЕФУцЛ§гыЫФБпаЮABCDЕФУцЛ§БШЮЊ3ЃК8ЃЛ
(4)ЁїMPAФмГЩЮЊЕШбќШ§НЧаЮЃЌЙВгаШ§жжЧщПіЃЌвдЯТЗжРрЫЕУїЃК
ЂйШєPMЃНPAЃЌ
ЁпPQЁЭMAЃЌ
ЁрЫФБпаЮABNQЪЧОиаЮЃЌ
ЁрQAЃНNBЃНtЃЌ
ЁрMQЃНQAЃНtЃЌ
гжЁпDM+MQ+QAЃНAD
Ёр3tЃН3ЃЌМДtЃН1
ЂкШєMPЃНMAЃЌдђMQЃН3Љ2tЃЌPQЃН![]() tЃЌMPЃНMAЃН3ЉtЃЌ
tЃЌMPЃНMAЃН3ЉtЃЌ
дкRtЁїPMQжаЃЌгЩЙДЙЩЖЈРэЕУЃКMP2ЃНMQ2+PQ2
Ёр(3Љt)2ЃН(3Љ2t)2+(![]() t)2ЃЌ
t)2ЃЌ
НтЕУЃКtЃН![]() (tЃН0ВЛКЯЬтвтЃЌЩсШЅ)ЃЛ
(tЃН0ВЛКЯЬтвтЃЌЩсШЅ)ЃЛ
ЂлШєAPЃНAMЃЌ
гЩЬтвтПЩЕУЃКAPЃН![]() tЃЌAMЃН3Љt
tЃЌAMЃН3Љt
Ёр![]() tЃН3ЉtЃЌ
tЃН3ЉtЃЌ
НтЕУЃКtЃН![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌЕБtЃН1ЛђtЃН![]() ЛђtЃН
ЛђtЃН![]() ЪБЃЌЁїMPAЪЧЕШбќШ§НЧаЮЃЎ
ЪБЃЌЁїMPAЪЧЕШбќШ§НЧаЮЃЎ


 ЬиИпМЖНЬЪІЕуВІЯЕСаД№АИ
ЬиИпМЖНЬЪІЕуВІЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌЕуDдкBCЩЯЃЌBD=DCЃЌЙ§ЕуDзїDEЁЭACЃЌДЙзуЮЊEЃЌЁбOОЙ§AЃЌBЃЌDШ§ЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКABЪЧЁбOЕФжБОЖЃЛ
ЃЈ2ЃЉХаЖЯDEгыЁбOЕФЮЛжУЙиЯЕЃЌВЂМгвджЄУїЃЛ
ЃЈ3ЃЉШєЁбOЕФАыОЖЮЊ3ЃЌЁЯBAC=60ЁуЃЌЧѓDEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
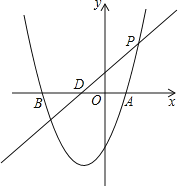
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНx2+bx+cгыxжсНЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉЃЌгыyжсНЛгкCЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЌВЂаДГіХзЮяЯпЕФЖдГЦжсЃЛ
ЃЈ2ЃЉЩшХзЮяЯпЕФЖдГЦжсНЛxжсгкDЃЌдкЖдГЦжсзѓВрЕФХзЮяЯпЩЯгавЛЕуEЃЌЪЙSЁїACEЃН![]() ЃЌЧѓЕуEЕФзјБъЃЛ
ЃЌЧѓЕуEЕФзјБъЃЛ
ЃЈ3ЃЉШєPЪЧжБЯпyЃНx+1ЩЯЕФвЛЕуЃЌPЕуЕФКсзјБъЮЊ![]() ЃЌMЪЧЕкЖўЯѓЯоХзЮяЯпЩЯЕФвЛЕуЃЌЕБЁЯMPDЃНЁЯADCЪБЃЌЧѓMЕуЕФзјБъЃЎ
ЃЌMЪЧЕкЖўЯѓЯоХзЮяЯпЩЯЕФвЛЕуЃЌЕБЁЯMPDЃНЁЯADCЪБЃЌЧѓMЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ4ЃЌЕуEЃЌFЗжБ№дкБпABЃЌADЩЯЃЌЧвЁЯECFЃН45ЁуЃЌCFЕФбгГЄЯпНЛBAЕФбгГЄЯпгкЕуGЃЌCEЕФбгГЄЯпНЛDAЕФбгГЄЯпгкЕуHЃЌСЌНгACЃЌEFЃЎЃЌGHЃЎ
ЃЈ1ЃЉЬюПеЃКЁЯAHCЁЁ ЁЁЁЯACGЃЛЃЈЬюЁАЃОЁБЛђЁАЃМЁБЛђЁАЃНЁБЃЉ
ЃЈ2ЃЉЯпЖЮACЃЌAGЃЌAHЪВУДЙиЯЕЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЩшAEЃНmЃЌ
ЂйЁїAGHЕФУцЛ§SгаБфЛЏТ№ЃПШчЙћБфЛЏЃЎЧыЧѓГіSгыmЕФКЏЪ§ЙиЯЕЪНЃЛШчЙћВЛБфЛЏЃЌЧыЧѓГіЖЈжЕЃЎ
ЂкЧыжБНгаДГіЪЙЁїCGHЪЧЕШбќШ§НЧаЮЕФmжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛДЮзлКЯЪЕМљПЮЩЯЃЌЭЌбЇУЧЮЊНЬЪвДАЛЇЩшМЦвЛИіекбєХёЃЌаЁУїЭЌбЇЛцжЦЕФЩшМЦЭМШчЭМЫљЪОЃЌЦфжаABБэЪОДАЛЇЃЌЧвABЃН2УзЃЌBCDБэЪОжБНЧекбєХюЃЌвбжЊЕБЕивЛФъжае§ЮчЪБПЬЬЋбєЙтгыЫЎЦНЯпCDЕФзюаЁМаНЧЁЯPDNЃН18.6ЁуЃЌзюДѓМаНЧЁЯMDNЃН64.5Ёу.ЧыФуИљОнвдЩЯЪ§ОнЃЌАяжњаЁУїЭЌбЇМЦЫуГіекбєХёжаCDЕФГЄЪЧЖрЩйУзЃПЃЈНсЙћОЋШЗЕН0.1ЃЉЃЈВЮПМЪ§ОнЃКsin18.6ЁуЁж0.32ЃЌtan18.6ЁуЁж0.34ЃЌsin64.5ЁуЁж0.90ЃЌtan64.5ЁуЁж2.1ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
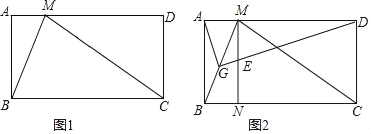
ЁОЬтФПЁПдкОиаЮABCDжаЃЌMЮЊADБпЩЯвЛЕуЃЌMBЦНЗжЁЯAMCЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКBCЃНMCЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌGЮЊBMЕФжаЕуЃЌСЌНгAGЁЂDGЃЌЙ§ЕуMзїMNЁЮABНЛDGгкЕуEЁЂНЛBCгкЕуNЃЎ
ЂйЧѓжЄЃКAGЁЭDGЃЛ
ЂкЕБDGGEЃН13ЪБЃЌЧѓBMЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќМИФъЙКЮяЕФжЇИЖЗНЪНШевцдіЖрЃЌФГЪ§бЇаЫШЄаЁзщОЭДЫНјааСЫГщбљЕїВщЃЎЕїВщНсЙћЯдЪОЃЌжЇИЖЗНЪНгаЃКAЮЂаХЁЂBжЇИЖБІЁЂCЯжН№ЁЂDЦфЫћЃЌИУаЁзщЖдФГГЌЪавЛЬьФкЙКТђепЕФжЇИЖЗНЪННјааЕїВщЭГМЦЃЌЕУЕНШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎ

ЧыФуИљОнЭГМЦЭМЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮвЛЙВЕїВщСЫЖрЩйУћЙКТђепЃП
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЛдкЩШаЮЭГМЦЭМжаAжжжЇИЖЗНЪНЫљЖдгІЕФдВаФНЧЮЊЁЁ ЁЁЖШЃЎ
ЃЈ3ЃЉШєИУГЌЪаетвЛжмФкга1600УћЙКТђепЃЌЧыФуЙРМЦЪЙгУAКЭBСНжжжЇИЖЗНЪНЕФЙКТђепЙВгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,вбжЊХзЮяЯпy=ax![]() +bx+cОЙ§A(-3,0),B(1,0),C(0,3)Ш§Еу,ЦфЖЅЕуЮЊD,ЖдГЦжсЪЧжБЯпl,lгыxжсНЛгкЕуH
+bx+cОЙ§A(-3,0),B(1,0),C(0,3)Ш§Еу,ЦфЖЅЕуЮЊD,ЖдГЦжсЪЧжБЯпl,lгыxжсНЛгкЕуH
(1)ЧѓИУХзЮяЯпЕФНтЮіЪН;
(2)ШєЕуPЪЧИУХзЮяЯпЖдГЦжсlЩЯЕФвЛИіЖЏЕу,ЧѓЁїPBCжмГЄЕФзюаЁжЕ;
(3)ШчЭМ(2),ШєBЪЧЯпЖЮADЩЯЕФвЛИіЖЏЕу(EгыA.DВЛжиКЯ),Й§EЕузїЦНаагкyжсЕФжБЯпНЛХзЮяЯпгкЕуF,НЛxжсгкЕуG,ЩшЕуEЕФКсзјБъЮЊm,ЁїADFЕФУцЛ§ЮЊS.
ЂйЧѓSгыmЕФКЏЪ§ЙиЯЕЪН
ЂкSЪЧЗёДцдкзюДѓжЕ?ШєДцдк,ЧѓГізюДѓжЕМАДЫЪБЕуEЕФзјБъ;ШєВЛДцдк,ЧыЫЕУїРэгЩЁЃ
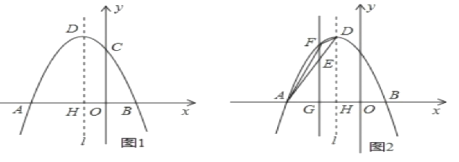
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШЋУцСНКЂеўВпЪЕЪЉКѓЃЌМзЃЌввСНИіМвЭЅгаСЫИїздЕФЙцЛЎ.МйЖЈЩњФаЩњХЎЕФИХТЪЯрЭЌЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉМзМвЭЅвбгавЛИіФаКЂЃЌзМБИдйЩњвЛИіКЂзгЃЌдђЕкЖўИіКЂзгЪЧХЎКЂЕФИХТЪЪЧ ЃЛ
ЃЈ2ЃЉввМвЭЅУЛгаКЂзгЃЌзМБИЩњСНИіКЂзгЃЌЧѓжСЩйгавЛИіКЂзгЪЧХЎКЂЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com