
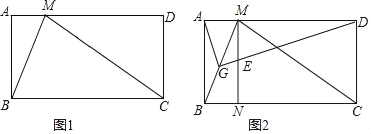
【题目】在矩形ABCD中,M为AD边上一点,MB平分∠AMC.
(1)如图1,求证:BC=MC;
(2)如图2,G为BM的中点,连接AG、DG,过点M作MN∥AB交DG于点E、交BC于点N.
①求证:AG⊥DG;
②当DGGE=13时,求BM的长.
【答案】(1)见解析;(2)①见解析;②2![]() .
.
【解析】
(1)根据平行线的性质得到∠AMB=∠MBC,根据角平分线的定义得到∠AMB=∠BMC,根据等腰三角形的判定定理证明;
(2)①连接GC,根据等腰三角形的三线合一得到∠BGC=90°,证明△AGD≌△BGC,根据全等三角形的性质证明;
②证明△MGE∽△DGM,根据相似三角形的性质计算即可.
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AMB=∠MBC,
∵MB平分∠AMC,
∴∠AMB=∠BMC,
∴∠BMC=∠MBC,
∴BC=MC;
(2)①证明:连接GC,
∵CM=CB,G为BM的中点,
∴∠BGC=90°,
∵∠BAM=90°,G为BM的中点,
∴GA=GB=GM,
∴∠GAB=∠GBA,
∴∠GAD=∠GBC,
在△AGD和△BGC中,
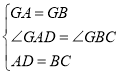 ,
,
∴△AGD≌△BGC(SAS),
∴∠AGD=∠BGC=90°,即AG⊥DG;
②解:∵MN∥AB,
∴∠MNB=90°,又∵∠BGC=90°,
∴∠BMN=∠BCG,
∵△AGD≌△BGC,
∴∠GDM=∠BCG,
∴∠BMN=∠GDM,又∠MGE=∠DGM,
∴△MGE∽△DGM,
∴![]() ,
,
∴MG2=DGGE=13,
∴MG=![]() ,
,
∴BM=2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
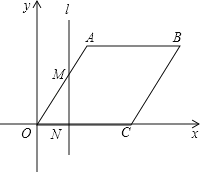
【题目】如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).
(1)求A、B两点的坐标;
(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;
(3)在题(2)的条件下,是否存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4?如果存在,请求出t的取值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 是常数)经过点
是常数)经过点![]() .
.
(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
①当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
②当点![]() 落在第二象限内,
落在第二象限内,![]() 取得最小值时,求
取得最小值时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把可以自由转动的圆形转盘A,B分别分成3等份的扇形区域,并在每一个小区域内标上数字.小明和小颖两个人玩转盘游戏,游戏规则是:同时转动两个转盘,当转盘停止时,若指针两区域的数字均为奇数,则小明胜;若指针两区域的数字均为偶数,则小颖胜;若有指针落在分割线上,则无效,需重新转动转盘.这个游戏规则对双方公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,AB=4cm,AD=3cm,动点M、N分别从D、B同时出发,都以1cm/秒的速度运动,点M沿DA向点终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于点P,连接MP,已知运动的时间为t秒(0<t<3).
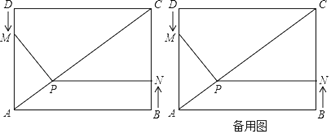
(1)当t=1秒时,求出PN的长;
(2)若四边形CDMP的面积为s,试求s与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t使四边形CDMP的面积与四边形ABCD的面积比为3:8,若存在,请求出t的值;若不存在,请说明理由.
(4)在点M、N运动过程中,△MPA能否成为一个等腰三角形?若能,试求出所有t的可能值;若不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4![]() ,BC=4,点D是AC的中点,点F是边AB上一动点,沿DF所在直线把△ADF翻折到△A′DF的位置,若线段A′D交AB于点E,且△BA′E为直角三角形,则BF的长为_____.
,BC=4,点D是AC的中点,点F是边AB上一动点,沿DF所在直线把△ADF翻折到△A′DF的位置,若线段A′D交AB于点E,且△BA′E为直角三角形,则BF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】主题班会课上,王老师出示了如图一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟,根据同学们的选择情况,小明绘制了如图两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
观点 | 频数 | 频率 |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |

(1)参加本次讨论的学生共有 人;
(2)表中a= ,b= ;
(3)将条形统计图补充完整;
(4)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
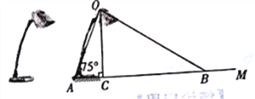
【题目】图为放置在水平桌面上的台灯的平面示意图,可伸缩式灯臂AO长为40 cm,与水平面所形成的夹角∠OAM恒为75°(不受灯臂伸缩的影响).由光源0射出的光线沿灯罩形成光线OC,OB,与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°.
(1)求该台灯照亮桌面的宽度BC.(不考虑其他因素,结果精确到1 cm,参考数据:sin75°≈0.97,cos75°≈0.26, ![]() ≈1.73)
≈1.73)
(2)若灯臂最多可伸长至60 cm,不调整灯罩的角度,能否让台灯照亮桌面85 cm的宽度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2-2mx+3(m>![]() )的图象与x轴交于点A(a,0)和点B(a+n,0)(n>0且n为整数),与y轴交于C点.
)的图象与x轴交于点A(a,0)和点B(a+n,0)(n>0且n为整数),与y轴交于C点.
(1)若a=1,①求二次函数关系式;②求△ABC的面积;
(2)求证:a=m-![]() ;
;
(3)线段AB(包括A、B)上有且只有三个点的横坐标是整数,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com