
����Ŀ����ͼ,��֪������y=ax![]() +bx+c����A(-3,0),B(1,0),C(0,3)����,�䶥��ΪD,�Գ�����ֱ��l,l��x�ύ�ڵ�H
+bx+c����A(-3,0),B(1,0),C(0,3)����,�䶥��ΪD,�Գ�����ֱ��l,l��x�ύ�ڵ�H
(1)��������ߵĽ���ʽ;
(2)����P�Ǹ������߶Գ���l�ϵ�һ������,���PBC�ܳ�����Сֵ;
(3)��ͼ(2),��B���߶�AD�ϵ�һ������(E��A.D���غ�),��E����ƽ����y���ֱ�߽��������ڵ�F,��x���ڵ�G,���E�ĺ�����Ϊm,��ADF�����ΪS.
����S��m�ĺ�����ϵʽ
��S�Ƿ�������ֵ?������,������ֵ����ʱ��E������;��������,��˵�����ɡ�
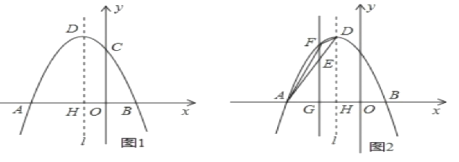
���𰸡���1��y=-x![]() -2x+3;��2��3
-2x+3;��2��3![]() +
+![]()
��3����![]() �ڣ�-2,2��
�ڣ�-2,2��
��������
(1)���ݺ���ͼ��������,�ô���ϵ����ȷ�����κ����Ľ���ʽ����;
(2)����BC�Ƕ�ֵ,�õ���PB+PC��Сʱ,��PBC���ܳ���С,���ݵ�����������Ӧ�߶εij�����;
(3)���E�ĺ�����Ϊm,��ʾ��E(m,2m+6),F(m,-m![]() -2m+3),����ʾ��EF�ij�,�Ӷ���ʾ
-2m+3),����ʾ��EF�ij�,�Ӷ���ʾ
��S��m�ĺ�����ϵ,Ȼ������κ�������ֵ���ɽ��
(1)�������֪

���: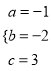
�������ߵĽ���ʽΪ:y=-x![]() -2x+3;
-2x+3;
��2������PBC���ܳ�Ϊ:PB+PC+BC
��BC�Ƕ�ֵ,
�൱PB+PC��Сʱ,��PBC���ܳ���С
�ߵ�A��B���ڶԳ���Գ�,

������AC��1�ڵ�P,����PΪ����ĵ�
.��AP= BP
����PBC���ܳ���С��:
PB+PC+BC=AC+BC
��A(-3,0),B(1,0),C(0,3),
��AC=3![]() BC=
BC=![]()
����PBC�ܳ�����СֵΪ3![]() +
+![]()
��3����:������y=-x![]() -2x+3;����D������Ϊ(-1,4)
-2x+3;����D������Ϊ(-1,4)
��A(-3,0)
��ֱ��AD�Ľ���ʽΪy=2x+6
�ߵ�E�ĺ�����Ϊm
��E(m,2m+6),F(m,-m![]() -2m+3
-2m+3
��EF=-m![]() -2m+3-(2m+6)=-m
-2m+3-(2m+6)=-m![]() -4m-3
-4m-3
��S= S��DEF+S��AEF=![]()
��![]()
�൱m=-2ʱ��S������ֵΪ1
��ʱ��E������Ϊ��-2,2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O������D��DE��AC��DE=![]() AC������AE��OD�ڵ�F������CE��OE��
AC������AE��OD�ڵ�F������CE��OE��
��1����֤��OE=CD��
��2��������ABCD�ı߳�Ϊ2����ABC=60�㣬��AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪ���Σ�AB��4cm��AD��3cm������M��N�ֱ��D��Bͬʱ����������1cm/����ٶ��˶�����M��DA����յ�A�˶�����N��BC���յ�C�˶�������N��NP��BC����AC�ڵ�P������MP����֪�˶���ʱ��Ϊt�루0��t��3����
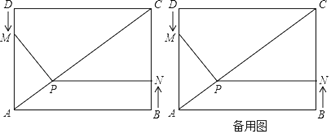
��1����t��1��ʱ�����PN�ij���
��2�����ı���CDMP�����Ϊs������s��t�ĺ�����ϵʽ��
��3�����˶������У��Ƿ����ijһʱ��tʹ�ı���CDMP��������ı���ABCD�������Ϊ3��8�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
��4���ڵ�M��N�˶������У���MPA�ܷ��Ϊһ�����������Σ����ܣ����������t�Ŀ���ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ϣ�����ʦ��ʾ����ͼһ������������ͬѧ�ǵ�һ�����飬��������ĸ��۵㣺
A���������ң��˴����أ� B���������棬�˴�ƽ�⣻
C�������Ը˴˳ɾͣ� D����������������˫Ӯ��
Ҫ��ÿ��ѡȡ����һ���۵�д���Լ��ĸ�����ͬѧ�ǵ�ѡ�������С����������ͼ������������ͼ���������ͼ�����ṩ����Ϣ������������⣺
�۵� | Ƶ�� | Ƶ�� |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |

��1���μӱ������۵�ѧ�������� ���ˣ�
��2������a���� ����b���� ����
��3��������ͳ��ͼ����������
��4��������A��B��C��D�ĸ��۵�����ѡ������Ϊ�ݽ����⣬�����б�����״ͼ�ķ�����ѡ�й۵�D����������������˫Ӯ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
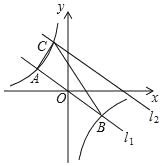
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��y=��![]() x�뷴��������y=
x�뷴��������y=![]() ��ͼ����A��B���㣨��A�ڵ�B��ࣩ����֪A�����������2��
��ͼ����A��B���㣨��A�ڵ�B��ࣩ����֪A�����������2��
��1�����������ı���ʽ��
��2����ֱ��l1��y=��![]() x����ƽ�ƺ��ֱ��l2�뷴��������y=
x����ƽ�ƺ��ֱ��l2�뷴��������y=![]() �ڵڶ������ڽ��ڵ�C�������ABC�����Ϊ30����ƽ�ƺ��ֱ��l2�ĺ�������ʽ��
�ڵڶ������ڽ��ڵ�C�������ABC�����Ϊ30����ƽ�ƺ��ֱ��l2�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
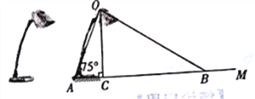
����Ŀ��ͼΪ������ˮƽ�����ϵ�̨�Ƶ�ƽ��ʾ��ͼ��������ʽ�Ʊ�AO��Ϊ40 cm,��ˮƽ�����γɵļнǡ�OAM��Ϊ75��(���ܵƱ�������Ӱ��).�ɹ�Դ0����Ĺ����ص����γɹ���OC��OB����ˮƽ�����γɵļнǡ�OCA,��OBA�ֱ�Ϊ90���30��.
(1)���̨����������Ŀ���BC.(�������������أ������ȷ��1 cm���ο�����:sin75���0.97,cos75���0.26�� ![]() ��1.73)
��1.73)
(2)���Ʊ������쳤��60 cm,���������ֵĽǶȣ��ܷ���̨����������85 cm�Ŀ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=8��PΪ�߶�AB�ϵ�һ�����㣬�ֱ���AP��PBΪ����AB��ͬ��������APCD������PBFE����P��C��E��һ��ֱ���ϣ���DAP=60�㣮M��N�ֱ��ǶԽ���AC��BE���е㣮����P���߶�AB���ƶ�ʱ����M��N֮��ľ������Ϊ�� ����
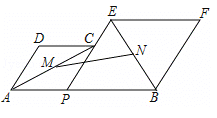
A. 2![]() B. 2
B. 2![]() C. 2D. 3
C. 2D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B�Ƿ���������y��![]() ��k��0��ͼ���ϵ����㣬�ӳ��߶�AB��y���ڵ�C���ҵ�BΪ�߶�AC�е㣬����A��AD��x���ڵ�D����EΪ�߶�OD�����ȷֵ㣬��OE��DE������AE��BE����S��ABE��7����k��ֵΪ�� ��
��k��0��ͼ���ϵ����㣬�ӳ��߶�AB��y���ڵ�C���ҵ�BΪ�߶�AC�е㣬����A��AD��x���ڵ�D����EΪ�߶�OD�����ȷֵ㣬��OE��DE������AE��BE����S��ABE��7����k��ֵΪ�� ��

A.��12B.��10C.��9D.��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x1��x2��һԪ���η��̣�a��6��x2+2ax+a=0������ʵ������
��1���Ƿ����ʵ��a��ʹ��x1+x1x2=4+x2�����������ڣ����a��ֵ���������ڣ�����˵�����ɣ�
��2����ʹ��x1+1����x2+1��Ϊ��������ʵ��a������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com