
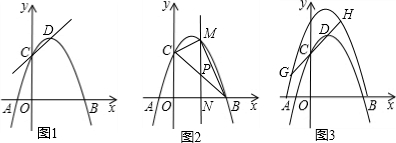
���� ��1���ɸ��ݽ���ʽֱ�ӵó�����D�����꣬�ֿɸ���CD�ij��ó�C�����꣬�������ʽ�м��ɵó�a��ֵ�����������ߵĽ���ʽ��
��2����P��x��-x+3������M��x��-x2+2x+3��������S��BCM=S��PMC+S��PMB������������κ�����ֵ��
��3�����ȵó���DHEΪ����ֱ�������Σ��������õ�H�������ߣ�y=-��x-1��2+4+m�ϣ��ó�4+$\frac{1}{2}$m=-��1+$\frac{1}{2}$m-1��2+4+m�����ɵó��𰸣�
��� 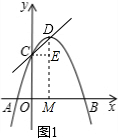 �⣺��1����ͼ1������D��DM��x���ڵ�M������C��CE��DM�ڵ�E��
�⣺��1����ͼ1������D��DM��x���ڵ�M������C��CE��DM�ڵ�E��
��y=a��x-1��2+4��
��ɵ��䶥��D����Ϊ��1��4����C��0��a+4����
��CE=1���ɹ��ɶ����ã�DE=1��
DE=DM-EM=4-��a+4��=1��
��a=-1
�������ߵĽ���ʽ��y=-x2+2x+3��
��2����ͼ2����P��x��-x+3������M��x��-x2+2x+3����
��PM=��-x2+2x+3��-��-x+3��=-x2+3x��
��S��BCM=S��PMC+S��PMB=$\frac{1}{2}$PM•NO+$\frac{1}{2}$PM•NB=$\frac{1}{2}$PM��NO+BN��=$\frac{1}{2}$PM•BO=$\frac{3}{2}$PM��
��S��BCM=$\frac{3}{2}$��-x2+3x��=-$\frac{3}{2}$��x-$\frac{3}{2}$��2+$\frac{27}{8}$��
�൱x=$\frac{3}{2}$ʱ����BCM��������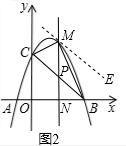
��N��$\frac{3}{2}$��0����
�ⷨ2����ͼ2����ΪBC��Ϊ��ֵ������BC�ϸ�Ҫ���BCƽ����������������ʱ�����
BC�Ľ���ʽy=-x+3����ME�Ľ���ʽy=-x+b
����y=-x2+2x+3��x2-3x+b-3=0��
���=b2-4ac=9-4��b-3��=0��
��ã�b=$\frac{21}{4}$��
��b=$\frac{21}{4}$ʱ������x2-3x+b-3=0��Ψһ���������Ϊ��$\frac{3}{2}$��
��N��$\frac{3}{2}$��0��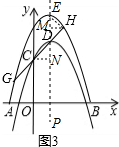 ��
��
��3����ͼ3���������ߵĶԳ���EP��CN��EP��N��HM��EP��M���ɣ�1���еá�DNCΪ����ֱ�������Σ�
���DHEҲΪ����ֱ�������Σ�
��EM=DM=HM=$\frac{1}{2}$m��
��H��1+$\frac{1}{2}$m��4+$\frac{1}{2}$m ����
�ߵ�H�������ߣ�y=-��x-1��2+4+m�ϣ�
��4+$\frac{1}{2}$m=-��1+$\frac{1}{2}$m-1��2+4+m��
��$\frac{1}{4}$m2=$\frac{1}{2}$m��
��m=2��m=0����ȥ��
��m��ֵΪ��m=2��
���� ���⿼���������߽���ʽ��ȷ�����������ɶ������������������֪ʶ�㣬����Ӧ�����ν���Լ�ͼ���ϵ�������ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��n����һ��һ�� | B�� | m��n�������� | ||
| C�� | m��n���Ǹ��� | D�� | m��n�п�����һ��Ϊ0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
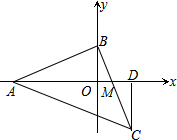 ��ͼ������Rt��ABC�У���ABC=90�㣬AB=BC����A��B�ֱ����������ϣ���x��ǡ��ƽ�֡�BAC��BC��x���ڵ�M����C����CD��x���ڵ�D����$\frac{CD}{AM}$��ֵΪ$\frac{1}{2}$��
��ͼ������Rt��ABC�У���ABC=90�㣬AB=BC����A��B�ֱ����������ϣ���x��ǡ��ƽ�֡�BAC��BC��x���ڵ�M����C����CD��x���ڵ�D����$\frac{CD}{AM}$��ֵΪ$\frac{1}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
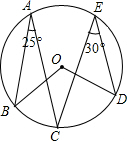 ��ͼ���ڡ�O�У�A��B��C��D����Բ�ϣ���BAC=25�㣬��CED=30�㣬���BOD�Ķ����ǣ�������
��ͼ���ڡ�O�У�A��B��C��D����Բ�ϣ���BAC=25�㣬��CED=30�㣬���BOD�Ķ����ǣ�������| A�� | 55�� | B�� | 110�� | C�� | 125�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
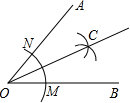 ��ͼ����ֱ�ߺ�Բ������AOB��ƽ���ߵ�ʾ��ͼ��ͼ��ʾ��������ѡ���У���˵��ͼ��������������OC�ǡ�AOB��ƽ���ߵ������ǣ�������
��ͼ����ֱ�ߺ�Բ������AOB��ƽ���ߵ�ʾ��ͼ��ͼ��ʾ��������ѡ���У���˵��ͼ��������������OC�ǡ�AOB��ƽ���ߵ������ǣ�������| A�� | SSS | |
| B�� | ASA | |
| C�� | AAS | |
| D�� | ��ƽ�������ĸ��ĵ㵽��������ߵľ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 32=6 | B�� | ��-$\frac{1}{4}$���£�-4��=1 | C�� | ��-8��2=-16 | D�� | -5-��-2��=-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
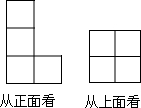 ��ͼ��ʾ���������ɸ���ȫ��ͬ��С�������ɵļ�����Ĵ�����ʹ����濴������״ͼ��������������������6��7��8��С�������ɵģ�
��ͼ��ʾ���������ɸ���ȫ��ͬ��С�������ɵļ�����Ĵ�����ʹ����濴������״ͼ��������������������6��7��8��С�������ɵģ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com