
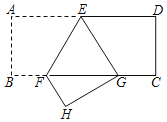
【题目】如图,矩形ABCD中,点E,F分别在AD,BC上,且AE=DE,BC=3BF,连接EF,将矩形ABCD沿EF折叠,点A恰好落在BC边上的点G处,则cos∠EGF的值为_____.
【答案】![]()
【解析】
连接AF,由矩形的性质得AD∥BC,AD=BC,由平行线的性质得∠AEF=∠GFE,由折叠的性质得∠AFE=∠GFE,AF=FG,推出∠AEF=∠AFE,则AF=AE,AE=FG,得出四边形AFGE是菱形,则AF∥EG,得出∠EGF=∠AFB,设BF=2x,则AD=BC=6x,AF=AE=FG=3x,在Rt△ABF中,cos∠AFB=![]() =
=![]() ,即可得出结果.
,即可得出结果.
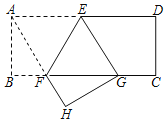
解:连接AF,如图所示:
∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
∴∠AEF=∠GFE,
由折叠的性质可知:∠AFE=∠GFE,AF=FG,
∴∠AEF=∠AFE,
∴AF=AE,
∴AE=FG,
∴四边形AFGE是菱形,
∴AF∥EG,
∴∠EGF=∠AFB,
设BF=2x,则AD=BC=6x,AF=AE=FG=3x,
在Rt△ABF中,cos∠AFB=![]() =
=![]() =
=![]() ,
,
∴cos∠EGF=![]() ,
,
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
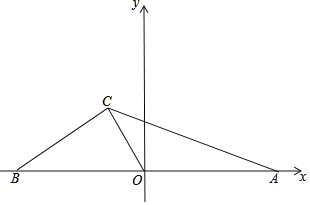
【题目】如图,在平面直角坐标系中,直线BC:y=![]() 交x轴于点B,点A在x轴正半轴上,OC为△ABC的中线,C的坐标为(m,
交x轴于点B,点A在x轴正半轴上,OC为△ABC的中线,C的坐标为(m,![]() )
)
(1)求线段CO的长;
(2)点D在OC的延长线上,连接AD,点E为AD的中点,连接CE,设点D的横坐标为t,△CDE的面积为S,求S与t的函数解析式;
(3)在(2)的条件下,点F为射线BC上一点,连接DB、DF,且∠FDB=∠OBD,CE=![]() ,求此时S值及点F坐标.
,求此时S值及点F坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
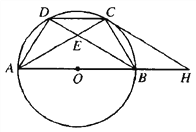
【题目】如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E。
(1)求证:DC2=CE·AC;
(2)若AE=2EC,求![]() 之值;
之值;
(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,若S△ACH=![]() ,求EC之长.
,求EC之长.
查看答案和解析>>
科目:初中数学 来源: 题型:
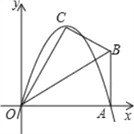
【题目】已知在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形,若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 于点D.
于点D.
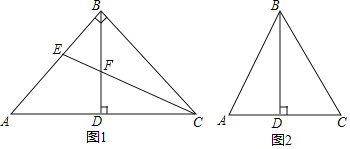
(1)如图1,当![]() 时,若CE平分
时,若CE平分![]() ,交AB于点E,交BD于点F.
,交AB于点E,交BD于点F.
①求证:![]() 是等腰三角形;
是等腰三角形;
②求证:![]() ;
;
(2)点E在AB边上,连接CE.若![]() ,在图2中补全图形,判断
,在图2中补全图形,判断![]() 与
与![]() 之间的数量关系,写出你的结论,并写出求解
之间的数量关系,写出你的结论,并写出求解![]() 与
与![]() 关系的思路.
关系的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A,B,C都在⊙O上,连接AB,AC,点D,E分别在AC,AB上,连接CE并延长交⊙O于点F,连接BD,BF,∠BDC﹣∠BFC=2∠ABF.
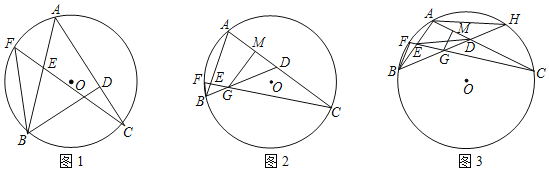
(1)如图1,求证:∠ABD=2∠ACF;
(2)如图2,CE交BD于点G,过点G作GM⊥AC于点M,若AM=MD,求证:AE=GD;
(3)如图3,在(2)的条件下,当AE:BE=8:7时,连接DE,且∠ADE=30°.延长BD交⊙O于点H,连接AH,AH=8![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,老师对大学说:“你任意想一个非零实数,然后按下列步骤操作,我会直接说出你运算的最后结果”
操作步骤如下:
第一步:计算这个数与1的和的平方,减去这个数与1的差的平方
第二步:把第一步得到的数乘以25
第三步:把第二步得到的数除以你想的这个数
(1)若小明同学心里想的是数9,请帮他计算出最后结果:
![]() .
.
(2)老师说:“同学们,无论你们心里想的是什么非零实数,按照以上步骤进行操作,得到的最后结果都相等”,小明同学想验证这个结论,于是,设心里想的数是a(a≠0),请你帮小明完成这个验证过程
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A![]() ,B(-1,2)是一次函数
,B(-1,2)是一次函数![]() 与反比例函数
与反比例函数![]()
(![]() )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是李老师在黑板上演示的尺规作图及其步骤,
已知钝角![]() ,尺规作图及步骤如下:
,尺规作图及步骤如下:
步骤一:以点![]() 为圆心,
为圆心,![]() 为半径画弧;
为半径画弧;
步骤二:以点![]() 为圆心,
为圆心,![]() 为半径画弧,两弧交于点
为半径画弧,两弧交于点![]() ;
;
步骤三:连接![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.

下面是四位同学对其做出的判断:
小明说:![]() ;
;
小华说:![]() ;
;
小强说:![]() ;
;
小方说:![]() .
.
则下列说法正确的是( )
A.只有小明说得对B.小华和小强说的都对
C.小强和小方说的都不对D.小明和小方说的都对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com