
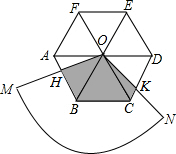
 如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.
如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.分析 (1)利用正六边形的性质得出△OBC,△OAB都是等边三角形,进而得出AO=CO,∠AOH=∠COK,∠OAH=∠OCK=60°,即可得出全等三角形;
(2)过点O作OG⊥BC于点G,利用全等三角形的性质以及正六边形性质得出正六边形ABCDEF与扇形OMN重叠部分的面积为:S△AOB+S△OBC=2SOBC进而得出答案.
解答 (1)证明:∵圆心角120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,
∴△OBC,△OAB都是等边三角形,
∴AO=CO,∠AOH=∠COK,∠OAH=∠OCK=60°,
在△AOH和△COK中,$\left\{\begin{array}{l}{∠AOH=∠COK}&{\;}\\{OA=OC}&{\;}\\{∠OAH=∠OCK}&{\;}\end{array}\right.$,
∴△AOH≌△COK(ASA);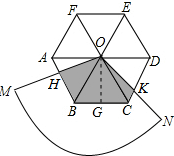
(2)解:过点O作OG⊥BC于点G,如图所示:
∵△OBC是等边三角形,
∴BG=CG=3,CO=6,
∴OG=3$\sqrt{3}$,
∵△AOH≌△COK,
∴S△AOH=S△COK,
∴正六边形ABCDEF与扇形OMN重叠部分的面积为:
S△AOB+S△OBC=2SOBC=2×$\frac{1}{2}$×6×3$\sqrt{3}$=18$\sqrt{3}$.
点评 此题主要考查了全等三角形的判定与性质以及正六边形的性质;证明三角形全等是解决问题的关键.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图:已知⊙P的半径为1,圆心P在抛物线y=x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为(0,-1)、($\sqrt{2}$,1)或(-$\sqrt{2}$,1).
如图:已知⊙P的半径为1,圆心P在抛物线y=x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为(0,-1)、($\sqrt{2}$,1)或(-$\sqrt{2}$,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
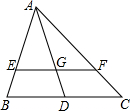 如图,△ABC中,EF∥BC,AD交EF于G.
如图,△ABC中,EF∥BC,AD交EF于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
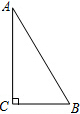 如图,在Rt△ABC中,∠C=90°,∠A=30°.
如图,在Rt△ABC中,∠C=90°,∠A=30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com