
分析 (1)先利用配方法得到y=2(x-$\frac{1}{2}$)2+$\frac{3}{2}$,则抛物线的顶点坐标为($\frac{1}{2}$,$\frac{3}{2}$),再利用点平移的规律得到点($\frac{1}{2}$,$\frac{3}{2}$)平移后的对应点的坐标为(-$\frac{1}{2}$,-$\frac{3}{2}$),于是利用顶点式可写出平移后的新抛物线的解析式;
(2)根据黄金抛物线写出的二次函数各项的系数满足b2=ac即可;
(3)由于△=b2-4ac,而b2=ac时,则△=-4ac,利用△=b2-4ac决定抛物线与x轴的交点个数进行讨论:当c=0时,△=0,该黄金抛物线与x轴只有一个公共点;当c≠0时,由于a、c同号,则△<0,则可判断该黄金抛物线与x轴没有公共点.
解答 解:(1)y=2x2-2x+2=2(x-$\frac{1}{2}$)2+$\frac{3}{2}$,则抛物线的顶点坐标为($\frac{1}{2}$,$\frac{3}{2}$),
把点($\frac{1}{2}$,$\frac{3}{2}$)先向下平移3个单位,再向左平移2个单位得到点(-$\frac{1}{2}$,-$\frac{3}{2}$),
所以平移后的新抛物线的解析式为y=2(x+$\frac{1}{2}$)2-$\frac{3}{2}$,即y=2x2+2x-1;
(2)抛物线y=2x2+2x+2是黄金抛物线;
(3)△=b2-4ac,
因为b2=ac时,
所以△=ac-4ac=-4ac,
当c=0时,△=0,该黄金抛物线与x轴只有一个公共点,即原点;
当c≠0时,而a、c同号,则△<0,所以该黄金抛物线与x轴没有公共点.
故答案为y=2x2+2x-1;y=2x2+2x+2.
点评 本题考查了抛物线与x轴的交点问题:对于二次函数y=ax2+bx+c(a、b、c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了抛物线的几何变换.


科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12% | B. | 30% | C. | 19% | D. | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-(x-3)=1 | B. | 3-2(x-3)=6 | C. | 2-3(x-3)=6 | D. | 3-2(x-3)=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
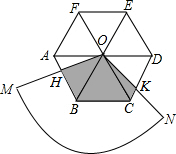 如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.
如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com