
| A. | 1-(x-3)=1 | B. | 3-2(x-3)=6 | C. | 2-3(x-3)=6 | D. | 3-2(x-3)=1 |
科目:初中数学 来源: 题型:解答题
| 上期抄见数 | 本期抄见数 | 加原表用水量(吨) | 本期用水量(吨) | ||
| 889 | 924 | 35 | 污水处理费 | ||
| 用水量(吨) | 单价元(/吨) | 金额(元) | 用水量(吨) | 单价元(/吨) | 金额(元) |
| 阶梯一20 | 1.30 | 26.00 | 20 | 0.50 | 10.00 |
| 阶梯二10 |  | 19.00 | 10 | 0.50 | 5.00 |
| 阶梯三5 |  | 15.00 | 5 | 0.50 | 2.50 |
| 本期实付金额(大写) | 柒拾柒元伍角整 77.50(元) | ||||
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 棱柱的侧面可以是正方形,也可以是三角形 | |
| B. | 一个几何体的表面不可能只有曲面组成 | |
| C. | 棱柱的各条棱都相等 | |
| D. | 圆锥是由平面和曲面组成的几何体 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图:已知⊙P的半径为1,圆心P在抛物线y=x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为(0,-1)、($\sqrt{2}$,1)或(-$\sqrt{2}$,1).
如图:已知⊙P的半径为1,圆心P在抛物线y=x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为(0,-1)、($\sqrt{2}$,1)或(-$\sqrt{2}$,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
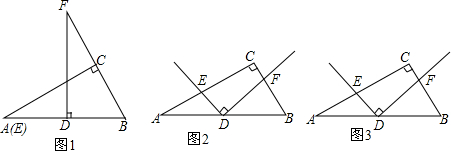
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com