
分析 (1)首先找出公式中的a,b,c的值,再代入求根公式求解即可.
(2)首先把括号内的分式进行通分,进行加法运算,然后把除法转化成乘法,进行乘法运算,然后把已知的式子求出a的值,代入化简以后的式子即可求解.
解答 解:(1)a=1,b=3,c=-2,
△=b2-4ac=9+8=17,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-3±\sqrt{17}}{2×1}$=$\frac{-3±\sqrt{17}}{2}$,
则:x1=$\frac{-3+\sqrt{17}}{2}$,x2=$\frac{-3-\sqrt{17}}{2}$
(2).解:原式=[$\frac{3}{(a+3)(a-3)}$+$\frac{a-3}{(a+3)(a-3)}$]÷$\frac{{a}^{2}}{a-3}$
=$\frac{a}{(a+3)(a-3)}$•$\frac{a-3}{{a}^{2}}$
=$\frac{1}{{a}^{2}+3a}$;
由a2+a=0,解得:a=0或-1,
当a=0时,原分式无意义,
当a=-1时,原式=$\frac{1}{1-3}$=-$\frac{1}{2}$.
点评 本题考查了分式的化简求值:先把分式的分子或分母因式分解,再进行通分或约分,得到最简分式或整式,然后把满足条件的字母的值代入计算得到对应的分式的值.由考查了公式法解一元二次方程.


科目:初中数学 来源: 题型:选择题
| A. | 12% | B. | 30% | C. | 19% | D. | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-(x-3)=1 | B. | 3-2(x-3)=6 | C. | 2-3(x-3)=6 | D. | 3-2(x-3)=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
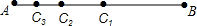 如图所示,AB=16cm,
如图所示,AB=16cm,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
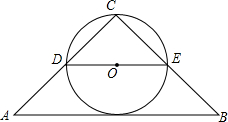 如图,在等腰Rt△ABC中,∠C=90°.点D,E分别为腰的中点,以DE长为直径作圆,圆心为O.请判断⊙O和底边AB是否相切,并说明理由.
如图,在等腰Rt△ABC中,∠C=90°.点D,E分别为腰的中点,以DE长为直径作圆,圆心为O.请判断⊙O和底边AB是否相切,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
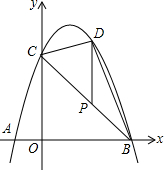 如图,抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3).
如图,抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com