
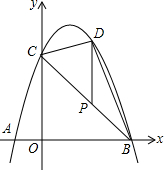
 如图,抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3).
如图,抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3).分析 (1)根据抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3),可以求得抛物线的表达式;
(2)根据函数的解析式可以求得点B的坐标,从而可以求得直线BC的解析式,设出点P、D的坐标从而可以表示出△BDC的面积,从而可以得到点P的坐标;
(3)根据题意可知AC可能为平行四边形的边,也可能为对角线,从而可以分为两种情况,从而可以分别求得点E、F的坐标.
解答 解:(1)∵点A(-1,0),点C(0,3)在抛物线y=-x2+bx+c上,
∴$\left\{\begin{array}{l}{-1-b+c=0}\\{c=3}\end{array}\right.$
解得b=2,c=3.
即抛物线的表达式是y=-x2+2x+3;
(2)令-x2+2x+3=0,解得x1=-1,x2=3,
∵点A(-1,0),
∴点B的坐标为(3,0).
设过点B、C的直线的解析式为:y=kx+b
$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得k=-1,b=3.
∴过点B、C的直线的解析式为:y=-x+3.
设点P的坐标为(a,-a+3),则点D的坐标为(a,-a2+2a+3),
∴PD=(-a2+2a+3)-(-a+3)=-a2+3a.
∴S△BDC=S△PDC+S△PDB
=$\frac{1}{2}PD•a+\frac{1}{2}PD•(3-a)$
=$\frac{1}{2}(-{a}^{2}+3a)•a+\frac{1}{2}(-{a}^{2}+3a)•(3-a)$
=$-\frac{3}{2}(a-\frac{3}{2})^{2}+\frac{27}{8}$.
∴当a=$\frac{3}{2}$时,△BDC的面积最大,
∴点P的坐标为($\frac{3}{2},\frac{3}{2}$).
(3)存在.
当AC是平行四边形的边时,则点E的纵坐标为3或-3,
∵E是抛物线上的一点,
∴将y=3代入y=-x2+2x+3,得x1=0(舍去),x2=2;
将y=-3代入y=-x2+2x+3,得${x}_{3}=1+\sqrt{7,}{x}_{4}=1-\sqrt{7}$.
∴${E}_{1}(2,3),{E}_{2}(1+\sqrt{7,-3}),{E}_{3}(1-\sqrt{7},-3)$.
则点${F}_{1}{(1,0),F}_{2}(2+\sqrt{7,0}){F}_{3}(2-\sqrt{7},0)$.
当AC为平行四边形的对角线时,则点E的纵坐标为3,
∵E是抛物线上的一点,
∴将y=3代入y=-x2+2x+3,得x1=0(舍去),x2=2;
即点E4(2,3).
则F4(-3,0).
由上可得,点E的坐标为:${E}_{1}(2,3),{E}_{2}(1+\sqrt{7,-3}),{E}_{3}(1-\sqrt{7},-3)$,E4(2,3),
与之对应的点F的坐标是:${F}_{1}{(1,0),F}_{2}(2+\sqrt{7,0}){F}_{3}(2-\sqrt{7},0)$,F4(-3,0).
点评 本题考查二次函数综合题,解题的关键是根据题意找出其中的相关联的量,利用分类讨论的数学思想解答各个问题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
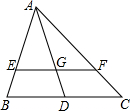 如图,△ABC中,EF∥BC,AD交EF于G.
如图,△ABC中,EF∥BC,AD交EF于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
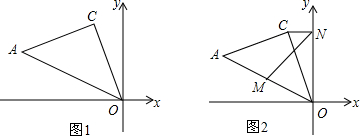
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
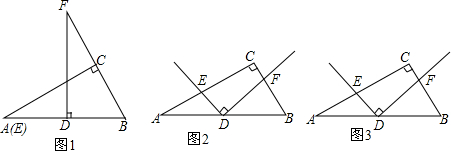
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2015 | B. | 1036 | C. | 518 | D. | 259 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )
已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )| A. | -a<-b<a<b | B. | a<-b<b<-a | C. | -b<a<-a<b | D. | a<b<-b<-a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com