
 如图:已知⊙P的半径为1,圆心P在抛物线y=x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为(0,-1)、($\sqrt{2}$,1)或(-$\sqrt{2}$,1).
如图:已知⊙P的半径为1,圆心P在抛物线y=x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为(0,-1)、($\sqrt{2}$,1)或(-$\sqrt{2}$,1). 分析 ⊙P与x轴相切时,则d=r=1,故此y=1或y=-1,然后将y=1或y=-1代入y=x2-1求得x的值,从而可求得点P的坐标.
解答 解:∵⊙P与x轴相切,
∴d=r=1,即点P的纵坐标为±1.
当y=1时,x2-1=1,解得:x=±$\sqrt{2}$,
∴点P的坐标为($\sqrt{2}$,1)或(-$\sqrt{2}$,1).
当y=-1时,x2-1=-1,解得x=0.
∴点P的坐标为(0,-1).
综上所述,点P的坐标为(0,-1)、($\sqrt{2}$,0)或(-$\sqrt{2}$,0).
故答案为:(0,-1)、($\sqrt{2}$,1)或(-$\sqrt{2}$,1).
点评 本题主要考查的是切线的性质,由切线的性质得到y=±1是解题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-(x-3)=1 | B. | 3-2(x-3)=6 | C. | 2-3(x-3)=6 | D. | 3-2(x-3)=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
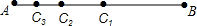 如图所示,AB=16cm,
如图所示,AB=16cm,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
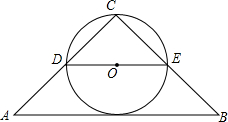 如图,在等腰Rt△ABC中,∠C=90°.点D,E分别为腰的中点,以DE长为直径作圆,圆心为O.请判断⊙O和底边AB是否相切,并说明理由.
如图,在等腰Rt△ABC中,∠C=90°.点D,E分别为腰的中点,以DE长为直径作圆,圆心为O.请判断⊙O和底边AB是否相切,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
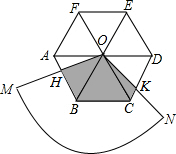 如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.
如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com