
【题目】某学校在“你最喜爱的课外活动项目”调查中,随机调查了若干名学生(每名学生分别选了一个活动项目),并根据调查结果绘制了如图所示的扇形统计图.已知“最喜爱机器人”的人数比“最喜爱3D打印”的人数少5人,则被调查的学生总人数为( )

A.50人B.40人C.30人D.25人
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】在我校举行的小科技创新发明比赛中,共有60人获奖,组委会原计划按照一等奖5人,二等奖15人,三等奖40人进行奖励.后来经学校研究决定,在该项奖励总奖金不变的情况下,各等级获奖人数实际调整为:一等奖10人,二等奖20人,三等奖30人,调整后一等奖每人奖金降低80元,二等奖每人奖金降低50元,三等奖每人奖金降低30元,调整前二等奖每人奖金比三等奖每人奖金多70元,则调整后一等奖每人奖金比二等奖每人奖金多____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别标有数字1、2、3的三张卡片洗匀后,背面朝上放在桌面上请完成下列各题
(1)随机抽取1张,求抽到卡片数字是奇数的概率;
(2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?
(3)在(2)的条件下,试求组成的两位数是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一节前夕,某商店从厂家购进![]() 两种礼盒,已知
两种礼盒,已知![]() 两种礼盒的单价比为
两种礼盒的单价比为![]() ,单价和为
,单价和为![]() 元
元
(1)求![]() 两种礼盒的单价分别是多少元?
两种礼盒的单价分别是多少元?
(2)该商店购进这两种礼盒恰好用去![]() 元,且购进
元,且购进![]() 种礼盒最多
种礼盒最多![]() 个,
个,![]() 种礼盒的数量不超过
种礼盒的数量不超过![]() 种礼盒数量的
种礼盒数量的![]() 倍,共有哪几种进货方案?
倍,共有哪几种进货方案?
(3)根据市场行情,销售一个![]() 种礼盒可获利
种礼盒可获利![]() 元,销售一个
元,销售一个![]() 种礼盒可获利
种礼盒可获利![]() 元.为奉献爱心,该商店决定每售出一个
元.为奉献爱心,该商店决定每售出一个![]() 种礼盒,为爱心公益基金捐款
种礼盒,为爱心公益基金捐款![]() 元,每个
元,每个![]() 种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,
种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,![]() 的值是多少?此时该商店可获利多少元?
的值是多少?此时该商店可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
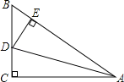
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论.①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB,其中正确的是____________
查看答案和解析>>
科目:初中数学 来源: 题型:
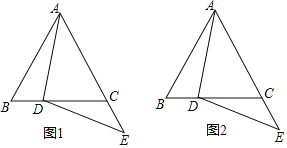
【题目】在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②小姚通过观察、实验提出猜想:在点D运动的过程中,始终有DA=AM,小姚把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明DA=AM,只需证△ADM是等边三角形;
想法2:连接CM,只需证明△ABD≌△ACM即可.
请你参考上面的想法,帮助小姚证明DA=AM(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
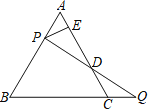
【题目】如图,过边长为2的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC边于D,则DE的长为( )
A.![]() B.1C.
B.1C.![]() D.不能确定
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com