
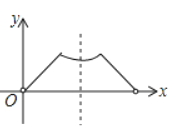
【题目】已知点P为某个封闭图形边界上一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )
A.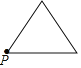 B.
B.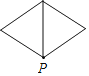 C.
C.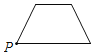 D.
D.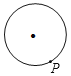
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】我市某乡镇实施产业精准扶贫,帮助贫困户承包了若干亩土地种植新品草莓,已知该草莓的成本为每千克10元,草莓成熟后投入市场销售,经市场调查发现,草莓销售不会亏本,且每天的销售量y(千克)与销售单价x(元/千克)之间函数关系如图所示.

(1)求y与x的函数关系式,并写出x的取值范围.
(2)当该品种草莓的定价为多少时,每天销售获得利润最大?最大利润是多少?
(3)某村今年草莓采摘期限30天,预计产量6000千克,则按照(2)中的方式进行销售,能否销售完这批草莓?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加,某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见表:
A型销售数量(台) | B型销售数量(台) | 总利润(元) |
5 | 3 | 950 |
3 | 4 | 900 |
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共80台,其中B型空气净化器的进货量不多于A型空气净化器的2倍,为使该公司销售完这80台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为200m3/小时,B型空气净化器的净化能力为300m3/小时,某长方体室内活动场地的总面积为200m2,室内墙高3m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,若不考虑空气对流等因素,至多要购买A型空气净化器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.
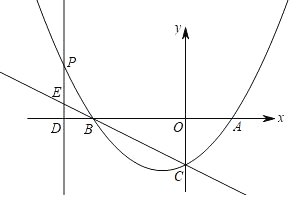
(1)求抛物线的函数表达式;
(2)若点P在第二象限内,且PE=![]() OD,求△PBE的面积.
OD,求△PBE的面积.
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.
(1)判断顶点M是否在直线y=4x+1上,并说明理由.
(2)如图1,若二次函数图象也经过点A,B,且mx+5>﹣(x﹣b)2+4b+1,根据图象,写出x的取值范围.
(3)如图2,点A坐标为(5,0),点M在△AOB内,若点C(![]() ,y1),D(
,y1),D(![]() ,y2)都在二次函数图象上,试比较y1与y2的大小.
,y2)都在二次函数图象上,试比较y1与y2的大小.
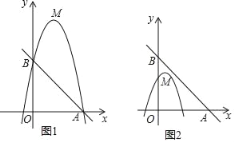
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,![]() 是
是![]() 的直径,点
的直径,点![]() 为
为![]() 上一点,
上一点,![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 的延长线上一点,且
的延长线上一点,且![]() .
.
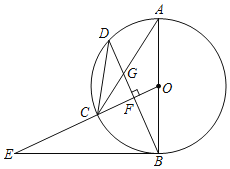
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若⊙O的半径为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25m,BD=1.5m,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
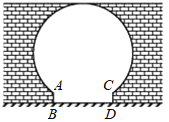
A.2mB.2.5mC.2.4mD.2.1m
查看答案和解析>>
科目:初中数学 来源: 题型:
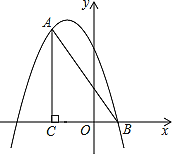
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com