
【题目】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25m,BD=1.5m,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
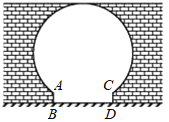
A.2mB.2.5mC.2.4mD.2.1m
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
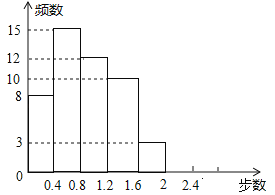
【题目】现今,“微信运动“被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况并进行统计整理,绘制了如下的统计图表(不完整):请根据以上信息,解答下列问题
(1)写出a,b的值并补全频数分布直方图;
(2)50名教师该日“微信运动”统计数据中步数的中位数落在第 组;本市约有40000名教师,估计日行走步数超过1.2万步(包含1.2万步)的教师约有 名.
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,求被选取的两名教师恰好都在2000步(包含20000)以上的概率.
步数(万步) | 频数 | 频率 |
0≤x<0.4 | 8 | a |
0.4≤x<0.8 | 15 | 0.3 |
0.8≤x<1.2 | 12 | 0.241 |
1.2≤x<1.6 | 10 | 0.2 |
1.6≤x<2 | 3 | 0.06 |
2≤x<2.4 | b | 0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:
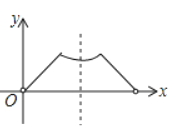
【题目】已知点P为某个封闭图形边界上一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )
A. B.
B.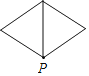 C.
C.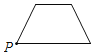 D.
D.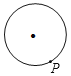
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,反比例函数y=![]() (x>0,k>0图象上的两点(n,3n)、(n+1,2n).
(x>0,k>0图象上的两点(n,3n)、(n+1,2n).
(1)求n的值;
(2)如图,直线l为正比例函数y=x的图象,点A在反比例函数y=![]() (x>0,k>0)的图象上,过点A作AB⊥l于点B,过点B作BC⊥x轴于点C,过点A作AD⊥BC于点D,记△BOC的面积为S1,△ABD的面积为S2,求S1﹣S2的值.
(x>0,k>0)的图象上,过点A作AB⊥l于点B,过点B作BC⊥x轴于点C,过点A作AD⊥BC于点D,记△BOC的面积为S1,△ABD的面积为S2,求S1﹣S2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店A类笔的标价是B类笔标价的1.2倍,某顾客用240元买笔,能单独购买A笔的数量恰好比单独购买B类笔的数量少4支.
(1)求A,B两类笔的标价;
(2)若A类笔的进价为8元/支,B类笔的进价为7元/支.文具店老板准备用不超过760元购进两类笔共100支,应如何进货才能获得最大利润?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
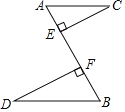
【题目】如图,两车从路段AB两端同时出发,沿平行路线行驶(即AC∥BD),CE和DF的长分别表示两车到道路AB的距离.
(1)如果两车行驶速度不相同,证明:△ACE∽△BDF;
(2)添加一个条件,使△ACE≌△BDF,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2011年高中招生考试,某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行,绘制成了如下两幅不完整的统计图,请根据图中所给信息,下列问题:
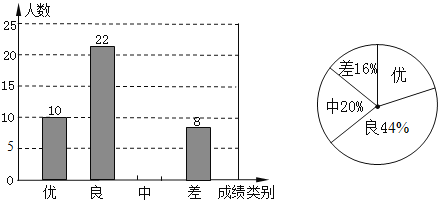
(1)请将表示成绩类别为“中”的条形统计图补充完整;
(2)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角是 72 度;
(3)学校九年级共有1000人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
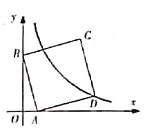
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,以
两点,以![]() 为边在第一象限作正方形
为边在第一象限作正方形![]() 沿
沿![]() 轴负方向平移
轴负方向平移![]() 个单位长度后,点
个单位长度后,点![]() 恰好落在双曲线上,则
恰好落在双曲线上,则![]() 的值是__________.
的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
(1)根据图象直接作答:a= ,b= ;
(2)求当x≥25时y与x之间的函数关系;
(3)把上述水费阶梯收费办法称为方案①,假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.(写出过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com