
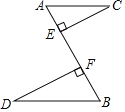
【题目】如图,两车从路段AB两端同时出发,沿平行路线行驶(即AC∥BD),CE和DF的长分别表示两车到道路AB的距离.
(1)如果两车行驶速度不相同,证明:△ACE∽△BDF;
(2)添加一个条件,使△ACE≌△BDF,请说明理由.
【答案】(1)见解析;(2)见解析.
【解析】
(1)直接利用平行线的性质以及相似三角形的判定方法进而得出答案;
(2)结合全等三角形的判定方法即可得出答案.
(1)证明:∵AC∥BD,
∴∠A=∠B,
∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°,
∴△ACE∽△BDF;
(2) 由(1)可知△ACE∽△BDF;如果相似比是1,则△ACE≌△BDF,所以需要有一条边相等,
我们发现决定两个三角形边长变化的是AC和BD的长度,
所以只要AC=BD,则可满足△ACE≌△BDF;
那么要使AC=BD,由已知可知两车同时出发,所以两车速度相同则可以保证AC=BD,
所以添加两车等速行驶即可
证明:∵AC∥BD,
∴∠A=∠B,
∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°,
∵两车等速同时行驶,
∴AC=BD,
在△ACE和△BDF中
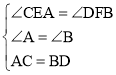 ,
,
∴△ACE≌△BDF(AAS).


科目:初中数学 来源: 题型:
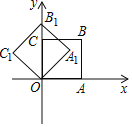
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
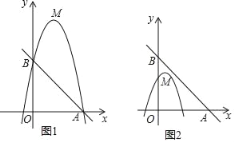
【题目】已知,点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.
(1)判断顶点M是否在直线y=4x+1上,并说明理由.
(2)如图1,若二次函数图象也经过点A,B,且mx+5>﹣(x﹣b)2+4b+1,根据图象,写出x的取值范围.
(3)如图2,点A坐标为(5,0),点M在△AOB内,若点C(![]() ,y1),D(
,y1),D(![]() ,y2)都在二次函数图象上,试比较y1与y2的大小.
,y2)都在二次函数图象上,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次,平均数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25m,BD=1.5m,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
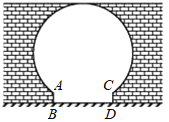
A.2mB.2.5mC.2.4mD.2.1m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,等腰△ODE中,OE=DE,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点B、E在反比例函数y=![]() 的图象上,OA=5,OC=1,则△ODE的面积为( )
的图象上,OA=5,OC=1,则△ODE的面积为( )
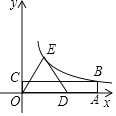
A.2.5B.5C.7.5D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20, A坐标为(-2,0),则顶点C的坐标为________.
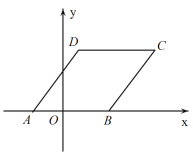
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ=![]() AB时,求tan∠CED的值;
AB时,求tan∠CED的值;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
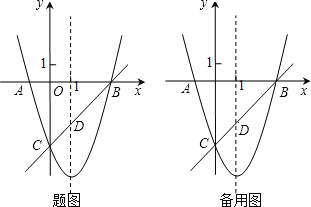
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)
阅读材料:
如图,在四边形ABCD中,对角线AC⊥BD,垂足为P.
求证:S四边形ABCD=![]()
证明:AC⊥BD→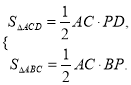
∴S四边形ABCD=S△ACD+S△ACB= ![]()
=![]()
解答问题:
(1)上述证明得到的性质可叙述为_______________________________________.
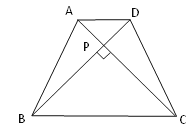
(2)已知:如图,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD且相交于点P,AD=3cm,BC=7cm,利用上述的性质求梯形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com