
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,P是BC边上一动点,设BP=x,若能在AC边上找一点Q,使∠BQP=90°,则x的范围是 . 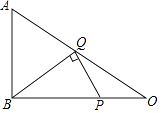
【答案】6≤x≤8
【解析】解:∵∠ABC=90°,AB=6,BC=8, ∴AC= ![]() =10,
=10,
∵∠BQP=90°,
∴点Q在以PB为直径的圆⊙M上,
∵点Q在AC上,
∴AC与⊙M相切于点Q,
连结MQ,如图,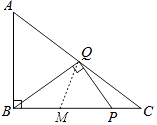
则MQ⊥AC,MQ=BM= ![]() x,
x,
∵∠QCM=∠BCA,
∴Rt△CMQ∽Rt△CAB,
∴QM:AB=CM:AC,即 ![]() x:6=(8﹣
x:6=(8﹣ ![]() x):10,
x):10,
∴x=6.
当P与C重合时,BP=8,
∴BP=x的取值范围是:6≤x≤8,
所以答案是:6≤x≤8.
【考点精析】本题主要考查了勾股定理的概念和相似三角形的判定与性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于O,EF经过点O,分别交AD,BC于E,F,已知ABCD的面积是![]() ,则图中阴影部分的面积是
,则图中阴影部分的面积是![]()
![]()

A. 12![]() B. 10
B. 10![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
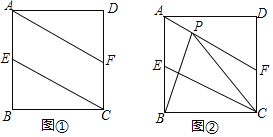
【题目】如图![]() ,矩形ABCD中,
,矩形ABCD中,![]() ,
,![]() ,E、F分别是AB、CD的中点
,E、F分别是AB、CD的中点
![]() 求证:四边形AECF是平行四边形;
求证:四边形AECF是平行四边形;
![]() 是否存在a的值使得四边形AECF为菱形,若存在求出a的值,若不存在说明理由;
是否存在a的值使得四边形AECF为菱形,若存在求出a的值,若不存在说明理由;
![]() 如图
如图![]() ,点P是线段AF上一动点且
,点P是线段AF上一动点且![]()
![]() 求证:
求证:![]() ;
;
![]() 直接写出a的取值范围.
直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=![]() ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市进行运河带绿化,计划种植银杏树苗,现甲、乙两家有相同的银杏树苗可供选择,其具体销售方案如下:
甲:购买树苗数量不超过500棵时,销售单价为800元![]() 棵;超过500棵的部分,销售单价为700元
棵;超过500棵的部分,销售单价为700元![]() 棵.
棵.
乙:购买树苗数量不超过1000棵时,销售单价为800元![]() 棵;超过1000棵的部分,销售单价为600元
棵;超过1000棵的部分,销售单价为600元![]() 棵.
棵.
设购买银杏树苗x棵,到两家购买所需费用分别为![]() 元、
元、![]() 元
元![]()
(1)该景区需要购买800棵银杏树苗,若都在甲家购买所要费用为______元,若都在乙家购买所需费用为______元;
(2)当![]() 时,分别求出
时,分别求出![]() 、
、![]() 与x之间的函数关系式;
与x之间的函数关系式;
(3)如果你是该景区的负责人,购买树苗时有什么方案,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
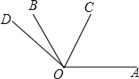
【题目】如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).
(1)当t为何值时,射线OC与OD重合;
(2)当t为何值时,∠COD=90°;
(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
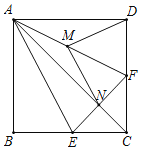
【题目】操作与证明:如图,把一个含![]() 角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、
角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、![]() 其中AC与EF交于点N,取AF中点M,连接MD、MN.
其中AC与EF交于点N,取AF中点M,连接MD、MN.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 在
在![]() 的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.
的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。
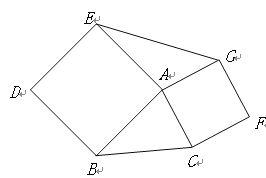
(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com