【题目】如图，以
为斜边作
和
，
，
，垂足为点
，点
是线段
上一点，连接
分别交
于
，过点
作
，交
延长线于点
，
．
（1）求证：
；
（2）若
，求
的长；
（3）若
，
，求线段
的长．
【答案】（1）详见解析；（2）
；（3）
【解析】
（1）由余角的性质可证
，由对顶角相等可得∠EAH=∠ADG，再由相似三角形的判定可得；
（2）由△AEH∽△BEG可得AE：BE=AH：BG，再由
，可得
，进而可求出AH；
（3）延长FE、BG，交于点M，作GN⊥EF于点N．由题意可得
，进而求出BM，z再由直角三角形的性质可得NG、FN；再证明△ENG∽△DFE，则
，设EF=a，进而求出a的值，即可得．
解：（1）证明:如图， 
，
，
．
，
，
，
，
；
（2）解：∵∠BFE=∠AEB=90°，
∴，
∵△AEH∽△BEG，
∴
，
∴，
∵BG=5，
∴
，
∴；
（3）如图，延长
、
，交于点
，
于点
，
，
，
，
，
．
，
∴点G为BM中点，
∴点N为AF的中点，
．
，
，
，
，
，
设
，
，
，
解得
，
．
科目：初中数学 来源： 题型：
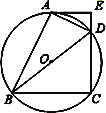
【题目】如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD交CD的延长线于点E，DA平分∠BDE．
⑴求证：AE是⊙O的切线；
⑵若AE＝4cm，CD＝6cm，求AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（阅读理解）
借助图形的直观性，我们可以直接得到一些有规律的算式的结果，比如：由图①，通过对小黑点的计数，我们可以得到1+2+3+…+n＝
n（n+1）；由图②，通过对小圆圈的计数，我们可以得到1+3+5+…+（2n﹣1）＝n2．
那么13+23+33+…+n3结果等于多少呢？
如图③，AB是正方形ABCD的一边，BB′＝n，B′B″＝n﹣1，B″B′′′＝n﹣2，……，显然AB＝1+2+3+…+n＝ n（n+1），分别以AB′、AB″、AB′′′、…为边作正方形，将正方形ABCD分割成块，面积分别记为Sn、Sn﹣1、Sn﹣2、…、S1．
（规律探究）
结合图形，可以得到Sn＝2BB′×BC﹣BB′2＝ ，
同理有Sn﹣1＝ ，Sn﹣2＝ ，…，S1＝13．
所以13+23+33+…+n3＝S四边形ABCD＝ ．
（解决问题）
根据以上发现，计算
的结果为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某超市购进某种水果的成本为20元/kg，经过市场调研发现，这种水果在未来40天的销售单价p（元/kg）与时间 t（天）之间的函数表达式为p＝
t+30；（1≤t≤40，t为整数），试销售当天（正式销售前一天）售出400kg，之后每天销售量比前一天减少5千克；
（1）试求每天销售利润W1（元）与时间t（天）之间的函数关系式；
（2）在销售前20天里，何时利润为4320元？
（3）为回馈新老顾客的支持，在实际销售中，超市决定每销售1kg水果就捐赠2元利润给“精准扶贫”对象．在日销售量不低于300kg的情况下，何时超市获利最多？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平行四边形ABCD中，点E在AD边上，连接BE、CE，EB平分∠AEC .
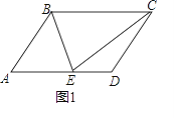
（1）如图1，判断△BCE的形状，并说明理由；
（2）如图2，若∠A=90°，BC=5，AE=1，求线段BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某学校为了了解九年级学生上学期间平均每天的睡眠情况，现从全校
名九年级学生中随机抽取了部分学生，调查了这些同学上学期间平均每天的睡眠时间
（单位：小时），并根据调查结果列出统计表，绘制成扇形统计图，如图所示．请你根据图表提供的信息解答下列问题：
平均每天睡眠时间分组统计表
组别序号 | 睡眠时间 | 人数（频数） |
|
|
|
|
|
|
|
|
|
|
|
|
平均每天睡眠时间扇形统计表
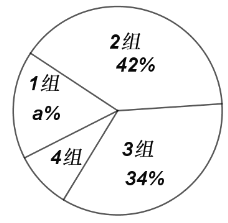
（1）
_______，
_______，
_______（
为百分号前的数字）；
（2）随机抽取的这部分学生平均每天睡眠时间的中位数落在_______组（填组别序号）；
（3）估计全校名九年级学生中平均每天睡眠时间不低于
小时的学生有_______名；
（4）若所抽查的睡眠时间
（小时）的
名学生，其中
名男生和名女生，现从这名学生中随机选取名学生参加个别访谈，请用列表或画树状图的方法求选取的名学生恰为
男女的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
