
【题目】某超市购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来40天的销售单价p(元/kg)与时间 t(天)之间的函数表达式为p=![]() t+30;(1≤t≤40,t为整数),试销售当天(正式销售前一天)售出400kg,之后每天销售量比前一天减少5千克;
t+30;(1≤t≤40,t为整数),试销售当天(正式销售前一天)售出400kg,之后每天销售量比前一天减少5千克;
(1)试求每天销售利润W1(元)与时间t(天)之间的函数关系式;
(2)在销售前20天里,何时利润为4320元?
(3)为回馈新老顾客的支持,在实际销售中,超市决定每销售1kg水果就捐赠2元利润给“精准扶贫”对象.在日销售量不低于300kg的情况下,何时超市获利最多?
【答案】(1)W1=﹣![]() t2+50t+4000;(2)在销售第8天时,利润为4320元;(3)当销售第20天时获利最大
t2+50t+4000;(2)在销售第8天时,利润为4320元;(3)当销售第20天时获利最大
【解析】
(1)根据总利润=每千克的利润×销售量可得函数解析式;
(2)将W1=4320代入函数解析式,解方程求出t的值,根据t<20可得答案;
(3)设此时获利W2元,由400﹣5t≥300知t≤20,根据“总利润=每千克的净利润×销售量”列出函数解析式,配方成顶点式后利用二次函数的性质求解可得.
解:(1)W1=(![]() t+30﹣20)(400﹣5t)
t+30﹣20)(400﹣5t)
=﹣![]() t2+50t+4000;
t2+50t+4000;
(2)当W1=4320时,﹣![]() t2+50t+4000=4320,
t2+50t+4000=4320,
解得t1=8,t2=32,
∵t<20,
∴t=8,
答:在销售第8天时,利润为4320元;
(3)设获利W2元,
由题意知400﹣5t≥300,
解得t≤20,
W2=(![]() t+30﹣20﹣2)(400﹣5t)
t+30﹣20﹣2)(400﹣5t)
=﹣![]() t2+60t+3200
t2+60t+3200
=﹣![]() (t﹣24)2+3920,
(t﹣24)2+3920,
∵a=﹣![]() <0,二次函数图象的开口向下,对称轴为直线t=24,
<0,二次函数图象的开口向下,对称轴为直线t=24,
∴当t<24时,W2随t的增大而增大,
∴当t=20时,W2有最大值,
答:当销售第20天时获利最大.


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
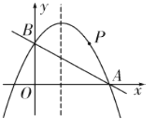
(1)求抛物线的解析式;
(2)若![]() 是抛物线上一点,且
是抛物线上一点,且![]() 点坐标为
点坐标为![]() ,点
,点![]() 为抛物线对称轴上一点,求
为抛物线对称轴上一点,求![]() 的最小值;
的最小值;
(3)点![]() 为直线
为直线![]() 上的动点,点
上的动点,点![]() 为抛物线上的动点,当以点
为抛物线上的动点,当以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,求点
为顶点的四边形是平行四边形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AB=10cm,AC=8cm,点P为边AC上一点,且AP=5cm.点Q为边AB上的任意一点(不与点A,B重合),若点A关于直线PQ的对称点A'恰好落在△ABC的边上,则AQ的长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以![]() 为斜边作
为斜边作![]() 和
和![]() ,
,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,点
,点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() 分别交
分别交![]() 于
于![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长;
的长;
(3)若![]()
![]() ,
,![]()
![]() ,求线段
,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
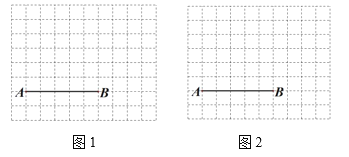
【题目】图1、图2分别是![]() 的网格,网格中每个小正方形的边长均为1,
的网格,网格中每个小正方形的边长均为1,![]() 、
、![]() 两点在小正方形的顶点上,请在图1、图2中各取一点
两点在小正方形的顶点上,请在图1、图2中各取一点![]() (点
(点![]() 必须在小正方形的顶点上),使以
必须在小正方形的顶点上),使以![]() 、
、![]() 、
、![]() 为顶点的三角形分别满足以下要求:
为顶点的三角形分别满足以下要求:
(1)在图1中画一个![]() ,使
,使![]() 是以
是以![]() 为斜边的直角三角形,且
为斜边的直角三角形,且![]() ;
;
(2)在图2中画一个![]() ,使
,使![]() 为等腰三角形,且
为等腰三角形,且![]() ,直接写出
,直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三(3)班学生的家距离学校人数的频数分布直方图如图所示,则下列说法中不正确的一项是( )
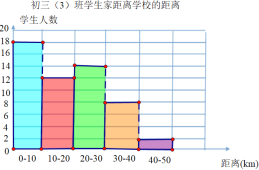
A.初三(3)班共有54名学生,其中家距离学校20-30km的学生人数为中位数.
B.初三(3)班学生的家距离学校为0-10km的学生人数的组中值为5km
C.初三(3)班学生的家距离学校为0-10km的学生人数为众数
D.初三(3)班学生的家距离学校各组数据的组中值的平均数为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
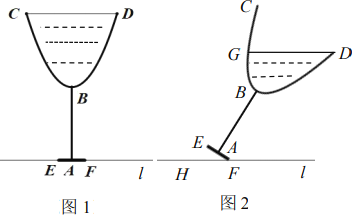
【题目】图1是一个高脚杯截面图,杯体![]() 呈抛物线状(杯体厚度不计),点
呈抛物线状(杯体厚度不计),点![]() 是抛物线的顶点,
是抛物线的顶点,![]() ,点
,点![]() 是
是![]() 的中点,当高脚杯中装满液体时,液面
的中点,当高脚杯中装满液体时,液面![]() ,此时最大深度(液面到最低点的距离)为
,此时最大深度(液面到最低点的距离)为![]() ,将高脚杯绕点
,将高脚杯绕点![]() 缓缓倾斜倒出部分液体,当
缓缓倾斜倒出部分液体,当![]() 时停止,此时液面为
时停止,此时液面为![]() ,则液面
,则液面![]() 到平面
到平面![]() 的距离是________________;此时杯体内液体的最大深度为_____________________.
的距离是________________;此时杯体内液体的最大深度为_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张矩形纸板和圆形纸板按如图方式分别剪得同样大定理特例图(AC=3,BC=4,AB=5,分别以三边长向外剪正方形) ,图1中边HI、LM和点K、J都恰好在矩形纸板的边上,图2中的圆心O在AB中点处,点H、I都在圆上,则矩形和圆形纸板的面积比是( )
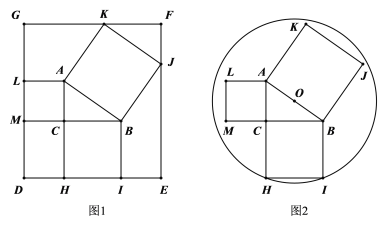
A.400:127πB.484:145πC.440:137πD.88:25π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com