
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
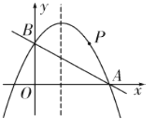
(1)求抛物线的解析式;
(2)若![]() 是抛物线上一点,且
是抛物线上一点,且![]() 点坐标为
点坐标为![]() ,点
,点![]() 为抛物线对称轴上一点,求
为抛物线对称轴上一点,求![]() 的最小值;
的最小值;
(3)点![]() 为直线
为直线![]() 上的动点,点
上的动点,点![]() 为抛物线上的动点,当以点
为抛物线上的动点,当以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,求点
为顶点的四边形是平行四边形时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)QP+QA的最小值为
;(2)QP+QA的最小值为![]() ;(3)满足条件的点M的坐标为
;(3)满足条件的点M的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先通过直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 计算出A、B点的坐标,再代入
计算出A、B点的坐标,再代入![]() 计算即可;
计算即可;
(2)根据对称性知A点关于抛物线对称轴的对称点是![]() ,连接PC,则QP+QA的最小值就是PC,从而计算即可;
,连接PC,则QP+QA的最小值就是PC,从而计算即可;
(3)根据平行四边形的性质分为以OB为边和对角线两种情况分类讨论计算.
(1)∵直线![]() 与x轴交于点A,与y轴交于点B
与x轴交于点A,与y轴交于点B
∴A(2,0),B(0,1)
∵抛物线y=-x2+bx+c经过A、B两点
∴![]()
∴![]()
∴抛物线解析式为![]()
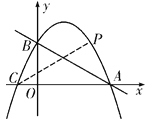
(2)如解图①,由(1)知,抛物线解析式为![]()
∴抛物线的对称轴为直线![]() ,
,
抛物线与x轴的另一交点为![]()
∵点A与点C关于对称轴对称
∴QP+QA的最小值
就是![]()
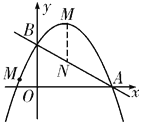
(3)①OB为平行四边形的边时,MN=OB,MN∥OB
∵点N在直线AB上
∴设![]()
∴![]()
∴![]()
Ⅰ.-m2+2m=1
解得,m=1
∴![]()
Ⅱ.-m2+2m=-1
解得,![]()
∴![]() 或
或![]()
②当OB为对角线时,OB与MN互相平分,交点为H,
∴OH=BH,MH=NH,
∵B(0,1),O(0,0),
∴![]() ,
,
设![]() ,
,![]() ,
,
∴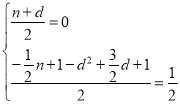 ,
,
∴ 或
或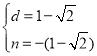 ,
,
∴![]() 或
或![]() ;
;
即:满足条件的点M的坐标为![]() 或
或![]() 或
或![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,在笔山银子岩坡顶![]() 处的同一水平面上有一座移动信号发射塔
处的同一水平面上有一座移动信号发射塔![]() ,
,
笔山职中数学兴趣小组的同学在斜坡底![]() 处测得该塔的塔顶
处测得该塔的塔顶![]() 的仰角为
的仰角为![]() ,然后他们沿着坡度为
,然后他们沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该塔的塔顶
处又测得该塔的塔顶![]() 的仰角为
的仰角为![]() .求:
.求:
![]() 坡顶
坡顶![]() 到地面
到地面![]() 的距离;
的距离;
![]() 移动信号发射塔
移动信号发射塔![]() 的高度(结果精确到
的高度(结果精确到![]() 米).
米).
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
(1)当![]() 时,
时,
①写出抛物线的对称轴;
②求抛物线的表达式;
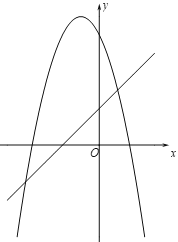
(2)存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,将点
,将点![]() 向右平移6个单位,得到点
向右平移6个单位,得到点![]() .
.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若抛物线![]() 经过点
经过点![]() ,
,![]() ,求该抛物线的表达式;
,求该抛物线的表达式;
(3)若抛物线![]() 的顶点在直线
的顶点在直线![]() 上移动,当抛物线与线段
上移动,当抛物线与线段![]() 有且只有一个公共点时,求抛物线顶点横坐标
有且只有一个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年疫情期间,为防止疫惰扩散,人们见面的机会少了,但是随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.为此,李老师设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),进行调查.将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次参与调查的共有_______人:在扇形统计图中,表示“微信”的扇形圆心角的度数为_______;其它沟通方式所占的百分比为_______;
(2)将条形统计图补充完整;
(3)如果我国有13亿人在使用手机.①请估计最喜欢用“微信”进行沟通的人数:并:用科学计数法表示;②在全国使用手机的人中随机抽取一人,用频率估计概率,求抽取的恰好使用“QQ”的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌和餐椅,已知每张餐椅的进价比每张餐桌的进价便宜110元,餐桌零售价270元/张,餐椅零售价70元/张.已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求该家具商场计划购进的餐桌、餐椅的进价分别为多少元?
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,售价500元/套,其余餐桌、餐椅以零售方式销售.请问该商场怎样进货,才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来40天的销售单价p(元/kg)与时间 t(天)之间的函数表达式为p=![]() t+30;(1≤t≤40,t为整数),试销售当天(正式销售前一天)售出400kg,之后每天销售量比前一天减少5千克;
t+30;(1≤t≤40,t为整数),试销售当天(正式销售前一天)售出400kg,之后每天销售量比前一天减少5千克;
(1)试求每天销售利润W1(元)与时间t(天)之间的函数关系式;
(2)在销售前20天里,何时利润为4320元?
(3)为回馈新老顾客的支持,在实际销售中,超市决定每销售1kg水果就捐赠2元利润给“精准扶贫”对象.在日销售量不低于300kg的情况下,何时超市获利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com