
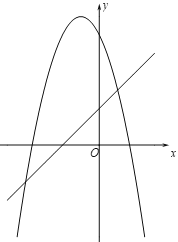
【题目】在平面直角坐标系中,点![]() ,将点
,将点![]() 向右平移6个单位,得到点
向右平移6个单位,得到点![]() .
.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若抛物线![]() 经过点
经过点![]() ,
,![]() ,求该抛物线的表达式;
,求该抛物线的表达式;
(3)若抛物线![]() 的顶点在直线
的顶点在直线![]() 上移动,当抛物线与线段
上移动,当抛物线与线段![]() 有且只有一个公共点时,求抛物线顶点横坐标
有且只有一个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据点A的坐标结合线段AB的长度,可得出点B的坐标;
(2)根据点A,B的坐标,利用待定系数法即可求出抛物线的表达式;
(3)将抛物线的表达式变形为顶点时,依此代入点A,B的坐标求出t的值,再结合图形即可得出:当抛物线与线段AB有且只有一个公共点时t的取值范围.
(1)∵点A的坐标为(-4,-2),将点A向右平移6个单位长度得到点B,
∴点B的坐标为(-4+6,-2),即(2,-2);
(2)将A(-4,-2),B(2,-2)代入![]() ,得:
,得:
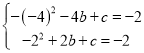 ,
,
解得:![]() ,
,
∴抛物线的表达式为![]() .
.
(3)∵抛物线![]() 的顶点在直线
的顶点在直线![]() 上移动,
上移动,
∴抛物线的顶点坐标为(![]() ,
,![]() ),
),
∴抛物线的表达式可化为![]() .
.
将A(-4,-2)代入![]() ,得:
,得:![]() ,
,
解得:![]() ,
,![]() ,
,
又∵抛物线与线段AB有且只有一个公共点,如图,
∴![]() ;
;
将B(2,-2)代入![]() ,得:
,得:![]() ,
,
解得![]() ,
,![]() ,
,
又∵抛物线与线段AB有且只有一个公共点,如图,
∴![]() .
.
综上可知,t的取值范围为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在标有平行四边形、矩形、菱形、正方形、等腰梯形、直角梯形的六张形状、大小完全相等的纸片中,连续抽取其中两张纸片,被抽中的(所对应的图形)恰好是轴对称的概率是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某调查机构对某地互联网行业从业情况进行调查统计,得到当地互联网行业从业人员年龄分布统计图和当地90后从事互联网行业岗位分布统计图:
互联网行业从业人员年龄分布统计图 90后从事互联网行业岗位分布图
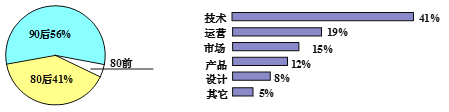
对于以下四种说法,你认为正确的是_____ (写出全部正确说法的序号).
①在当地互联网行业从业人员中,90后人数占总人数的一半以上
②在当地互联网行业从业人员中,80前人数占总人数的13%
③在当地互联网行业中,从事技术岗位的90后人数超过总人数的20%
④在当地互联网行业中,从事设计岗位的90后人数比80前人数少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 交
交![]() 于点
于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 垂直平分
垂直平分![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的是( )
.其中正确的是( )
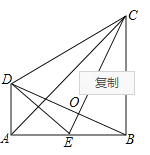
A.①②③B.①③⑤C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
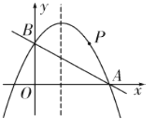
(1)求抛物线的解析式;
(2)若![]() 是抛物线上一点,且
是抛物线上一点,且![]() 点坐标为
点坐标为![]() ,点
,点![]() 为抛物线对称轴上一点,求
为抛物线对称轴上一点,求![]() 的最小值;
的最小值;
(3)点![]() 为直线
为直线![]() 上的动点,点
上的动点,点![]() 为抛物线上的动点,当以点
为抛物线上的动点,当以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,求点
为顶点的四边形是平行四边形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过![]() 时,材料温度降为600℃.如图,煅烧时温度
时,材料温度降为600℃.如图,煅烧时温度![]() 与时间
与时间![]() 成一次函敷关系:锻造时,温度
成一次函敷关系:锻造时,温度![]() 与时间
与时间![]() 成反比例函数关系。已知该材料初始温度是32℃.
成反比例函数关系。已知该材料初始温度是32℃.
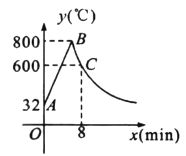
(1)分别求出材料煅烧和锻造时![]() 与
与![]() 的函数关系式,并且写出自变量
的函数关系式,并且写出自变量![]() 的取值范围;
的取值范围;
(2)根据工艺要求,当材料温度低于400℃时,须停止操作.那么锻造的操作时间最多有多长?.
(3)如果加工每个零件需要锻造12分钟,并且当材料温度低于400℃时,需要重新煅烧.通过计算说明加工第一个零件,一共需要多少分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2分别是![]() 的网格,网格中每个小正方形的边长均为1,
的网格,网格中每个小正方形的边长均为1,![]() 、
、![]() 两点在小正方形的顶点上,请在图1、图2中各取一点
两点在小正方形的顶点上,请在图1、图2中各取一点![]() (点
(点![]() 必须在小正方形的顶点上),使以
必须在小正方形的顶点上),使以![]() 、
、![]() 、
、![]() 为顶点的三角形分别满足以下要求:
为顶点的三角形分别满足以下要求:
(1)在图1中画一个![]() ,使
,使![]() 是以
是以![]() 为斜边的直角三角形,且
为斜边的直角三角形,且![]() ;
;
(2)在图2中画一个![]() ,使
,使![]() 为等腰三角形,且
为等腰三角形,且![]() ,直接写出
,直接写出![]() 的长度.
的长度.
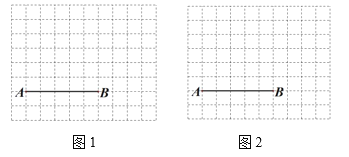
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com