
����Ŀ����������ij�ֽ�������Ҫ���в������պͶ�������������Ҫ�������յ�800�棬Ȼ��ֹͣ���ս��ж������������![]() ʱ�������¶Ƚ�Ϊ600�森��ͼ������ʱ�¶�
ʱ�������¶Ƚ�Ϊ600�森��ͼ������ʱ�¶�![]() ��ʱ��
��ʱ��![]() ��һ�κ����ϵ������ʱ���¶�
��һ�κ����ϵ������ʱ���¶�![]() ��ʱ��
��ʱ��![]() �ɷ�����������ϵ����֪�ò��ϳ�ʼ�¶���32�森
�ɷ�����������ϵ����֪�ò��ϳ�ʼ�¶���32�森
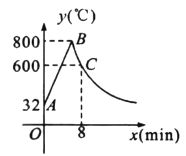
��1���ֱ�����������պͶ���ʱ![]() ��
��![]() �ĺ�����ϵʽ������д���Ա���
�ĺ�����ϵʽ������д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2�����ݹ���Ҫ�������¶ȵ���400��ʱ����ֹͣ��������ô����IJ���ʱ������ж����
��3������ӹ�ÿ�������Ҫ����12���ӣ����ҵ������¶ȵ���400��ʱ����Ҫ�������գ�ͨ������˵���ӹ���һ�������һ����Ҫ���ٷ��ӣ�
���𰸡���1��![]() ��
��![]() ����2������һ�β���ʱ��Ϊ6���ӣ���3���ӹ���һ�����һ����Ҫ
����2������һ�β���ʱ��Ϊ6���ӣ���3���ӹ���һ�����һ����Ҫ![]() ���ӣ�
���ӣ�
��������
��1������ʱ����![]() �������������������ʽ����
�������������������ʽ����![]() ʱ�������B�����꣬Ȼ��������ʱһ�κ���Ϊ
ʱ�������B�����꣬Ȼ��������ʱһ�κ���Ϊ![]() �������B�������һ�κ�������ʽ�������һ�κ����ͷ����������Ա���
�������B�������һ�κ�������ʽ�������һ�κ����ͷ����������Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ���뷴������������ʽ�����x��ֵ�ټ�ȥ��6���ӿ�ʼ���죬���ɵó��𰸣�
���뷴������������ʽ�����x��ֵ�ټ�ȥ��6���ӿ�ʼ���죬���ɵó��𰸣�
��3����һ�ζ�����Ҫ6���ӣ��ڶ��������Ǵ�400�����յ�800�棬��![]() ʱ������һ�κ�������ʽ��������յ�ʱ�䣬��������ӹ���һ����������ʱ�䣮
ʱ������һ�κ�������ʽ��������յ�ʱ�䣬��������ӹ���һ����������ʱ�䣮
(1)���϶���ʱ����![]() ���������
���������![]() �����
�����![]() ��
��
��![]() ʱ��
ʱ��![]() �����
�����![]() ��
��
���![]() ������Ϊ(6��800)����������ʱ����
������Ϊ(6��800)����������ʱ����![]() ��
��
�������![]() �����
�����![]() ��
��
���������ʱ��![]() ��
��![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ��
��
���϶���ʱ![]() ��
��![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]()
(2)��![]() ����
����![]() ����
����![]() ��
��
![]() ����:����һ�β���ʱ��Ϊ6���ӣ�
����:����һ�β���ʱ��Ϊ6���ӣ�
(3)��![]() ʱ��
ʱ��![]() ��
��
�����ÿ�������Ҫ�������Σ���һ��������Ҫ6���ӣ��ڶ������մ�400�����յ�800�棬
��![]() ʱ������
ʱ������![]() ��
��![]() ����ʱ
����ʱ![]() ��
��
��ӹ���һ�����һ����Ҫ![]() ���ӣ�
���ӣ�


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ����ֱ�ǵĶ���E����������ABCD�ĶԽ���AC�ϣ�ʹ�ǵ�һ�߽�CD�ڵ�F����һ�߽�CB�����ӳ����ڵ�G����![]() ��ֵ��
��ֵ��
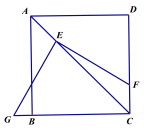
��2����ͼ������1���е���������ABCD���ij�������ABCD���������������䣮��AB��m��BC��n������![]() ��ֵ��
��ֵ��
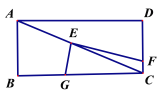
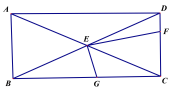
��3����ͼ����ֱ�Ƕ���E���ھ���ABCD�ĶԽ��߽��㣬EF��EG�ֱ�CD��CB�ڵ�F��G����ECƽ�֡�FEG����AB��2��BC��4��ֱ��д��EG��EF �ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AEƽ�֡�BAC��BC�ڵ�E��D��AB����һ���㣬����CD��AE�ڵ�P������BP����֪AB =6cm����B��D�����ľ���Ϊxcm��B��P�����ľ���Ϊy1cm��A��P�����ľ���Ϊy2cm��
С������ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
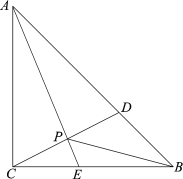
������С����̽�����̣��벹������:
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y1��![]() ��x�ļ����Ӧֵ��
��x�ļ����Ӧֵ��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 2.49 | 2.64 | 2.88 | 3.25 | 3.80 | 4.65 | 6.00 |
y2/cm | 4.59 | 4.24 | 3.80 | 3.25 | 2.51 | 0.00 |
��2����ͬһƽ��ֱ������ϵxOy�У������ȫ��ı��и�����ֵ����Ӧ�ĵ�(x��y1)��(x��![]() )������������y1��
)������������y1��![]() ��ͼ��
��ͼ��

��3����Ϻ���ͼ�ش��������⣺
�ٵ�AP=2BDʱ��AP�ij���ԼΪ cm��
�ڵ�BPƽ�֡�ABCʱ��BD�ij���ԼΪ cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҩ����Ҫ��������һ������Ч�������¹ڷ�������ҩƷ��Ҫ�������12�죨��12�죩����ɣ�Ϊ�˼ӿ������������ȡ���˼Ӱ࣬������ͣ��������ʽ������ÿ��ҩƷ�IJ���![]() ���֣���ʱ��
���֣���ʱ��![]() ���죩��һ�κ��������������±�������Ӧ��������ϵ�����ڻ���������ת������ģ�ƽ������ÿ��ҩƷ�ijɱ�
���죩��һ�κ��������������±�������Ӧ��������ϵ�����ڻ���������ת������ģ�ƽ������ÿ��ҩƷ�ijɱ�![]() ��Ԫ����ʱ��
��Ԫ����ʱ��![]() ���죩�Ĺ�ϵ������ͼ��ʾ�ĺ���ͼ��
���죩�Ĺ�ϵ������ͼ��ʾ�ĺ���ͼ��
ʱ�� | 2 | 4 |
ÿ����� | 24 | 28 |
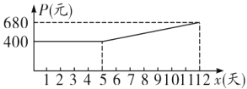
��1����ҩƷÿ��IJ���![]() ���֣���ʱ��
���֣���ʱ��![]() ���죩֮��ĺ�����ϵʽ��
���죩֮��ĺ�����ϵʽ��
��2����![]() ʱ��ֱ��д��
ʱ��ֱ��д��![]() ��Ԫ����ʱ��
��Ԫ����ʱ��![]() ���죩�ĺ�����ϵ��
���죩�ĺ�����ϵ��![]() ��
��
��3��������ҩƷ�ļ۸�Ϊ1400Ԫ/�֣�ÿ���������Ϊ![]() Ԫ������һ���������ߣ���������Ƕ��٣�������
Ԫ������һ���������ߣ���������Ƕ��٣�������![]() �ۼ�
�ۼ�![]() �ɱ���
�ɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���![]() ������
������![]() ����ƽ��6����λ���õ���
����ƽ��6����λ���õ���![]() ��
��
(1)ֱ��д����![]() �����ꣻ
�����ꣻ
(2)��������![]() ������
������![]() ��
��![]() ����������ߵı���ʽ��
����������ߵı���ʽ��
(3)��������![]() �Ķ�����ֱ��
�Ķ�����ֱ��![]() ���ƶ��������������߶�
���ƶ��������������߶�![]() ����ֻ��һ��������ʱ���������߶��������
����ֻ��һ��������ʱ���������߶��������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
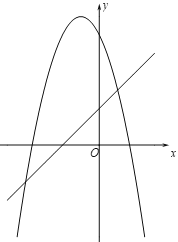
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬ![]() �У�
��![]() ��
��![]() ��
��![]() �DZ�
�DZ�![]() ��һ�㣬����
��һ�㣬����![]() ���۵���ֽƬ��ʹ��
���۵���ֽƬ��ʹ��![]() ����
����![]() �ϵ�
�ϵ�![]() �㣬��ʹ�ۺ۾�����
�㣬��ʹ�ۺ۾�����![]() ���õ��ۺ�
���õ��ۺ�![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() �ij��� ��
�ij��� ��
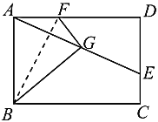
A.![]() B.4C.3D.2
B.4C.3D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
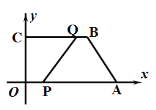
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���OABC�Ķ�������ֱ�ΪO��0��0����A��12��0����B��8��6����C��0��6��������P�ӵ�O��������ÿ��3����λ���ȵ��ٶ��ر�OA���յ�A�˶�������Q�ӵ�Bͬʱ��������ÿ��2����λ���ȵ��ٶ��ر�BC���յ�C�˶������˶���ʱ��Ϊt�룬��AG��PQ�ڵ�G����AG�����ֵΪ�� ��
A.![]() B.
B.![]() C.
C.![]() D.6
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
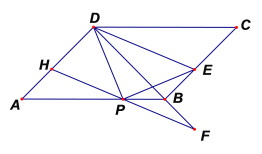
����Ŀ����ͼ����ƽ���ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��һ���㣬��
��һ���㣬��![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() ��
��![]() ����
����![]() �۵��õ�
�۵��õ�![]() ���ӳ�
���ӳ�![]() ��
��![]() ��
��![]() ������
������![]() ��
��
(1)��֤��![]() ��
��
(2)��![]() ʱ��֤��
ʱ��֤��![]() �ǵ��������Σ�
�ǵ��������Σ�
(3)��![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A(t��y1)��B(t+2��y2)��������y����![]() x2��ͼ���ϣ��ҩ�2��t��2�����߶�AB�������ֵ______.
x2��ͼ���ϣ��ҩ�2��t��2�����߶�AB�������ֵ______.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com