
【题目】如图,在平行四边形![]() 中,点
中,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() .
.
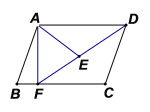
(1)求证:![]() ∽
∽![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90,D为AB的中点,AE∥DC,CE∥DA.
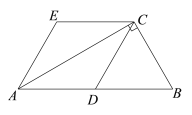
(1)求证:四边形ADCE是菱形;
(2)连接DE,若AC =![]() ,BC =2,求证:△ADE是等边三角形.
,BC =2,求证:△ADE是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是同-种蔬菜的两种裁植方法.甲:![]() 四珠顺次连结成为一个菱形,且
四珠顺次连结成为一个菱形,且![]() .乙:
.乙:![]() 四株连结成一个正方形。其中两行作物间的距离为行距;一行中相邻两株作物的距离为株距:设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积。设株距都为
四株连结成一个正方形。其中两行作物间的距离为行距;一行中相邻两株作物的距离为株距:设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积。设株距都为![]() ,其它客观因素都相同.则对于下列说法:
,其它客观因素都相同.则对于下列说法:
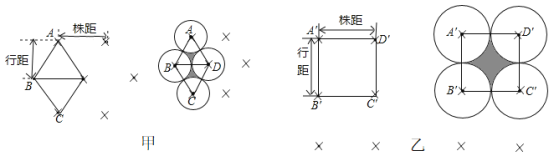
①甲的行距比乙的小;②甲的行距为![]() ;③甲、乙两种栽植方式,蔬菜形成的影子面积相同;④甲的空隙地面积比乙的空隙地面积少
;③甲、乙两种栽植方式,蔬菜形成的影子面积相同;④甲的空隙地面积比乙的空隙地面积少![]() .其中正确的个数为( )
.其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
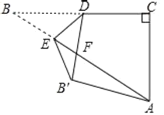
【题目】如图,在Rt△ABC中,∠C=90°,BC=4![]() ,AC=4,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若∠AB′F为直角,则AE的长为__________.
,AC=4,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若∠AB′F为直角,则AE的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
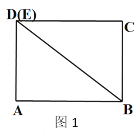
【题目】在综合与实践课上,老师组织同学们以“三角形纸片的旋转”为主题开展数学活动.如图1,现有矩形纸片ABCD,AB=8cm,AD=6cm.连接BD,将矩形ABCD沿BD剪开,得到△ABD和△BCE.保持△ABD位置不变,将△BCE从图1的位置开始,绕点B按逆时针方向旋转,旋转角为α(0°≤α<360°).在△BCE旋转过程中,边CE与边AB交于点F.
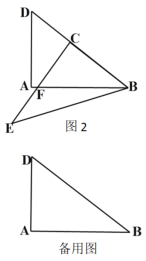
(1)如图2,将图1中的△BCE旋转到点C落在边BD上时,CF= ;
(2)继续旋转△BCE,当点E落在DA延长线上时,求出CF的长;
(3)在△BCE旋转过程中,连接AE,AC,当AC=AE时,直接写出此时α的度数及△AEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,AB是⊙O的直径,G为弦AE的中点,连接OG并延长交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为5,tanA=![]() ,求FD的长.
,求FD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以![]() 为斜边作
为斜边作![]() 和
和![]() ,
,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,点
,点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() 分别交
分别交![]() 于
于![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长;
的长;
(3)若![]()
![]() ,
,![]()
![]() ,求线段
,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒
方向以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动(点
运动(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 作
作![]() 交折线
交折线![]() 于点
于点![]() 以
以![]() 为边问下作正方形
为边问下作正方形![]() 点
点![]() 落在边
落在边![]() 上设点
上设点![]() 运动的时间为
运动的时间为![]() (秒).
(秒).

(1)直接用含![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
(2)当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的值.
的值.
(3)当正方形![]() 与
与![]() 重叠部分图形为四边形时,设四边形的面积为
重叠部分图形为四边形时,设四边形的面积为![]() (平方单位),求
(平方单位),求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)点![]() 为边
为边![]() 的中点,直接写出直线
的中点,直接写出直线![]() 将正方形
将正方形![]() 分成的两部分图形的面积比为
分成的两部分图形的面积比为![]() 时
时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com