
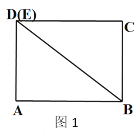
ΓΨΧβΡΩΓΩ‘ΎΉέΚœ”κ ΒΦυΩΈ…œΘ§άœ ΠΉι÷·Ά§―ßΟ«“‘ΓΑ»ΐΫ«–Έ÷ΫΤ§ΒΡ–ΐΉΣΓ±ΈΣ÷ςΧβΩΣ’Ι ΐ―ßΜνΕ·Θ°»γΆΦ1Θ§œ÷”–ΨΊ–Έ÷ΫΤ§ABCDΘ§ABΘΫ8cmΘ§ADΘΫ6cmΘ°Ν§Ϋ”BDΘ§ΫΪΨΊ–ΈABCD―ΊBDΦτΩΣΘ§ΒΟΒΫΓςABDΚΆΓςBCEΘ°±Θ≥÷ΓςABDΈΜ÷Ο≤Μ±δΘ§ΫΪΓςBCE¥”ΆΦ1ΒΡΈΜ÷ΟΩΣ ΦΘ§»ΤΒψBΑ¥Ρφ ±’κΖΫœρ–ΐΉΣΘ§–ΐΉΣΫ«ΈΣΠΝΘ®0ΓψΓήΠΝΘΦ360ΓψΘ©Θ°‘ΎΓςBCE–ΐΉΣΙΐ≥Χ÷–Θ§±ΏCE”κ±ΏABΫΜ”ΎΒψFΘ°
Θ®1Θ©»γΆΦ2Θ§ΫΪΆΦ1÷–ΒΡΓςBCE–ΐΉΣΒΫΒψC¬δ‘Ύ±ΏBD…œ ±Θ§CF= ΘΜ
Θ®2Θ©ΦΧ–χ–ΐΉΣΓςBCEΘ§Β±ΒψE¬δ‘ΎDA―”≥ΛœΏ…œ ±Θ§«σ≥ωCFΒΡ≥ΛΘΜ
Θ®3Θ©‘ΎΓςBCE–ΐΉΣΙΐ≥Χ÷–Θ§Ν§Ϋ”AEΘ§ACΘ§Β±ACΘΫAE ±Θ§÷±Ϋ”–¥≥ω¥Υ ±ΠΝΒΡΕ» ΐΦΑΓςAECΒΡΟφΜΐΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©CF=
ΘΜΘ®2Θ©CF=![]() ΘΜΘ®3Θ©60Γψ Θ§
ΘΜΘ®3Θ©60Γψ Θ§![]() Μρ 300ΓψΘ§
Μρ 300ΓψΘ§![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”Ο![]() Φ¥Ω…ΒΟ
Φ¥Ω…ΒΟ![]() ,¥ζ»κΦΤΥψΦ¥Ω…ΘΜ
,¥ζ»κΦΤΥψΦ¥Ω…ΘΜ
Θ®2Θ©“Ή÷ΛEF=FBΘ§‘Ό‘ΎRtBCF÷–άϊ”ΟΙ¥Ι…Ε®άμΦΤΥψΦ¥Ω…«σ≥ωCFΘΜ
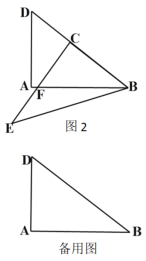
Θ®3Θ©Ζ÷E‘ΎCΒΡΉσ”“ΝΫ±ΏΝΫ÷÷«ιΩωΧ÷¬έΓΘE‘ΎCΒΡΉσ±Ώ ±Θ§…ηECΒΡ÷–ΒψΈΣGΘ§Ν§Ϋ”AGΘ§ΙΐΒψAΉςAHΓΆBC”ΎΒψHΘ°Ϋβ÷±Ϋ«»ΐΫ«–Έ«σ≥ωAGΦ¥Ω…ΫβΨωΈ ΧβΘΜE‘ΎCΒΡ”“±Ώ ±Θ§»ΓCEΒΡ÷–ΒψGΘ§Ν§Ϋ”AGΘ§ΉςBHΓΆAG”ΎHΘ°«σ≥ωAGΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®1Θ©ΓΏΓœCBF =ΓœCEB
Γύ![]()
Γύ![]()
ΓΏABΘΫEC=8Θ§ADΘΫBC=6
Γύ![]()
Γύ![]()
Ȯ2ȩÿBE=BDȧ BAâDE
ΓύΓœDBA=ΓœEBA
ΓΏ ΓœDBA =ΓœCEB
Γύ ΓœEBA=ΓœCEB
Γύ EF=FB
…ηCF=xΘ§‘ρ‘ΎRtBCF÷–Θ§
Θ®8©¹xΘ©2=62+ x2Θ§
ΫβΒΟx=![]()
Γύ CF=![]()
Θ®3Θ©E‘ΎCΉσ±Ώ ±Θ§»γΆΦ3÷–Θ§…ηECΒΡ÷–ΒψΈΣGΘ§Ν§Ϋ”AGΘ§ΙΐΒψAΉςAHΓΆBC”ΎΒψHΘ°
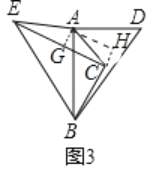
ΓΏACΘΫAEΘ§EGΘΫGCΘ§
ΓύAGΓΆECΘ§
ΓΏΓœGCHΘΫ180Γψ©¹ΓœECBΘΫ180Γψ©¹90ΓψΘΫ90ΓψΘ§
ΓύΓœAGCΘΫΓœGCHΘΫΓœAHCΘΫ90ΓψΘ§ΓύΥΡ±Ώ–ΈAGCH «ΨΊ–ΈΘ§
ΓύGCΘΫAHΘΫ![]() ECΘΫ
ECΘΫ![]() 8ΘΫ4
8ΘΫ4
‘ΎRtΓςABH÷–Θ§BHΘΫ![]() ΘΫ
ΘΫ![]() ΘΫ4
ΘΫ4![]() Θ§
Θ§
¥Υ ±![]()
Γύ![]() =30Γψ
=30Γψ
ΓύΠΝ=90-![]() =60Γψ
=60Γψ
ΓΏAGΘΫCHΘΫBH©¹BCΘΫ4![]() ©¹6Θ§
©¹6Θ§
ΓύSΓςAECΘΫ![]() ECAGΘΫ
ECAGΘΫ![]() ΓΝ8ΓΝΘ®4
ΓΝ8ΓΝΘ®4![]() ©¹6Θ©ΘΫΘ®16
©¹6Θ©ΘΫΘ®16![]() ©¹24Θ©cm2Θ°
©¹24Θ©cm2Θ°
E‘ΎC”“±Ώ ±Θ§»γΆΦ4Υυ ΨΘ§»ΓCEΒΡ÷–ΒψGΘ§Ν§Ϋ”AGΘ§ΉςBHΓΆAG”ΎHΘ°
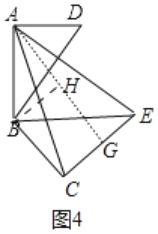
Ά§Ζ®Ω…ΒΟΘΚGHΘΫBCΘΫ6Θ§AHΘΫ4![]() Θ§
Θ§
ΓύAGΘΫAH+GHΘΫ4![]() +6Θ§
+6Θ§
ΓύSΓςAECΘΫ![]() ECAGΘΫ
ECAGΘΫ![]() ΓΝ8ΓΝΘ®4
ΓΝ8ΓΝΘ®4![]() +6Θ©ΘΫΘ®16
+6Θ©ΘΫΘ®16![]() +24Θ©cm2Θ°
+24Θ©cm2Θ°
¥Υ ±![]()
Γύ![]() =60Γψ
=60Γψ
ΓύΠΝ=360-![]() =30Γψ
=30Γψ
Ήέ…œΥυ ωΠΝ=60Γψ ±Θ§SΓςAECΘΫ![]() ΜρΠΝ=300Γψ ±Θ§SΓςAECΘΫ
ΜρΠΝ=300Γψ ±Θ§SΓςAECΘΫ![]() Θ°
Θ°


 ΜΞΕ·ΩΈΧΟœΒΝ–¥πΑΗ
ΜΞΕ·ΩΈΧΟœΒΝ–¥πΑΗ ΦΛΜνΥΦΈ§÷«Ρή―ΒΝΖΩΈ ±ΒΦ―ßΝΖœΒΝ–¥πΑΗ
ΦΛΜνΥΦΈ§÷«Ρή―ΒΝΖΩΈ ±ΒΦ―ßΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΒΡΗΚΑκ÷αΫΜ”ΎΒψ
÷αΒΡΗΚΑκ÷αΫΜ”ΎΒψ![]() Θ§”κ
Θ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§Ν§Ϋα
Θ§Ν§Ϋα![]() Θ§ΒψC(6Θ§
Θ§ΒψC(6Θ§![]() )‘Ύ≈ΉΈοœΏ…œΘ§÷±œΏ
)‘Ύ≈ΉΈοœΏ…œΘ§÷±œΏ![]() ”κ
”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]()
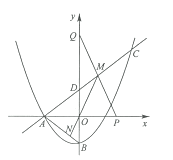
(1)«σ![]() ΒΡ÷ΒΦΑ÷±œΏ
ΒΡ÷ΒΦΑ÷±œΏ![]() ΒΡΚ· ΐ±μ¥ο ΫΘΜ
ΒΡΚ· ΐ±μ¥ο ΫΘΜ
(2)Βψ![]() ‘Ύ
‘Ύ![]() ÷α’ΐΑκ÷α…œΘ§Βψ
÷α’ΐΑκ÷α…œΘ§Βψ![]() ‘Ύ
‘Ύ![]() ÷α’ΐΑκ÷α…œΘ§Ν§Ϋα
÷α’ΐΑκ÷α…œΘ§Ν§Ϋα![]() ”κ÷±œΏ
”κ÷±œΏ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§Ν§Ϋα
Θ§Ν§Ϋα![]() ≤Δ―”≥ΛΫΜ
≤Δ―”≥ΛΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§»τ
Θ§»τ![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ°
ΒΡ÷–ΒψΘ°
ΔΌ«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
ΔΎ…ηΒψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡ≥Λ(”ΟΚ§
ΒΡ≥Λ(”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ Ψ)Θ°
ΒΡ¥ζ ΐ Ϋ±μ Ψ)Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΒγΤς…Χ≥Γœζ έΟΩΧ®ΫχΦέΖ÷±πΈΣ200‘ΣΓΔ170‘ΣΒΡAΓΔBΝΫ÷÷–ΆΚ≈ΒΡΒγΖγ…»Θ§œ¬±μ «ΗΟ–ΆΚ≈ΒγΖγ…»ΫϋΝΫ÷ήΒΡœζ έ«ιΩωΘΚ
œζ έ ±ΕΈ | œζ έ ΐΝΩ | œζ έ ’»κ | |
A÷÷–ΆΚ≈ | B÷÷–ΆΚ≈ | ||
ΒΎ“Μ÷ή | 3Χ® | 5Χ® | 1800‘Σ |
ΒΎΕΰ÷ή | 4Χ® | 10Χ® | 3100‘Σ |
![]() «σAΓΔBΝΫ÷÷–ΆΚ≈ΒΡΒγΖγ…»ΒΡœζ έΒΞΦέΘΜ
«σAΓΔBΝΫ÷÷–ΆΚ≈ΒΡΒγΖγ…»ΒΡœζ έΒΞΦέΘΜ
![]() »τΗΟ…Χ≥ΓΉΦ±Η”Ο≤ΜΕύ”Ύ5400‘ΣΒΡΫπΕν‘Ό≤…ΙΚ’βΝΫ÷÷–ΆΚ≈ΒΡΒγΖγ…»Ι≤30Χ®Θ§ΦΌ…η έΦέ≤Μ±δΘ§Ρ«Ο¥…Χ≥Γ”Π≤…”ΟΡΡ÷÷≤…ΙΚΖΫΑΗΘ§≤≈Ρή ΙΒΟΒ±œζ έΆξ’β–©Ζγ…»ΚσΘ§…Χ≥ΓΜώάϊΉνΕύΘΩΉνΕύΩ…ΜώάϊΕύ…Ό‘ΣΘΩ
»τΗΟ…Χ≥ΓΉΦ±Η”Ο≤ΜΕύ”Ύ5400‘ΣΒΡΫπΕν‘Ό≤…ΙΚ’βΝΫ÷÷–ΆΚ≈ΒΡΒγΖγ…»Ι≤30Χ®Θ§ΦΌ…η έΦέ≤Μ±δΘ§Ρ«Ο¥…Χ≥Γ”Π≤…”ΟΡΡ÷÷≤…ΙΚΖΫΑΗΘ§≤≈Ρή ΙΒΟΒ±œζ έΆξ’β–©Ζγ…»ΚσΘ§…Χ≥ΓΜώάϊΉνΕύΘΩΉνΕύΩ…ΜώάϊΕύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§–ΓΟς”Ο“Μ’≈±Ώ≥ΛΈΣ![]() ΒΡ’ΐ»ΐΫ«–Έ”≤÷ΫΑε…ηΦΤ“ΜΗωΈόΗ«ΒΡ’ΐ»ΐάβ÷υΧ«ΙϊΚ–Θ§¥”»ΐΗωΫ«¥ΠΖ÷±πΦτ»Ξ“ΜΗω–ΈΉ¥¥σ–ΓœύΆ§ΒΡΥΡ±Ώ–ΈΘ§Τδ“Μ±Ώ≥ΛΦ«ΈΣ
ΒΡ’ΐ»ΐΫ«–Έ”≤÷ΫΑε…ηΦΤ“ΜΗωΈόΗ«ΒΡ’ΐ»ΐάβ÷υΧ«ΙϊΚ–Θ§¥”»ΐΗωΫ«¥ΠΖ÷±πΦτ»Ξ“ΜΗω–ΈΉ¥¥σ–ΓœύΆ§ΒΡΥΡ±Ώ–ΈΘ§Τδ“Μ±Ώ≥ΛΦ«ΈΣ![]() Θ§‘Ό’έ≥…»γΆΦ2Υυ ΨΒΡΈόΗ«Χ«ΙϊΚ–Θ§ΥϋΒΡ»ίΜΐΦ«ΈΣ
Θ§‘Ό’έ≥…»γΆΦ2Υυ ΨΒΡΈόΗ«Χ«ΙϊΚ–Θ§ΥϋΒΡ»ίΜΐΦ«ΈΣ![]() Θ°
Θ°
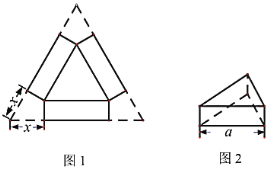
Θ®1Θ©![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΙΊœΒ Ϋ «__________Θ§Ή‘±δΝΩ
ΒΡΚ· ΐΙΊœΒ Ϋ «__________Θ§Ή‘±δΝΩ![]() ΒΡ»Γ÷ΒΖΕΈß «__________Θ°
ΒΡ»Γ÷ΒΖΕΈß «__________Θ°
Θ®2Θ©ΈΣΧΫΨΩ![]() Υφ
Υφ![]() ΒΡ±δΜ·Ιφ¬…Θ§–ΓΟςάύ±»Εΰ¥ΈΚ· ΐΫχ––ΝΥ»γœ¬ΧΫΨΩΘΚ
ΒΡ±δΜ·Ιφ¬…Θ§–ΓΟςάύ±»Εΰ¥ΈΚ· ΐΫχ––ΝΥ»γœ¬ΧΫΨΩΘΚ
ΔΌΝ–±μΘΚ«κΡψ≤Ι≥δ±μΗώ÷–ΒΡ ΐΨίΘΚ
| 0 | 0Θ°5 | 1 | 1Θ°5 | 2 | 2Θ°5 | 3 |
| 0 | 3Θ°125 | ________ | 3Θ°375 | ________ | 0Θ°625 | 0 |
ΔΎΟηΒψΘΚ«κΡψΑ―…œ±μ÷–ΗςΉιΕ‘”Π÷ΒΉςΈΣΒψΒΡΉχ±ξΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Οη≥ωœύ”ΠΒΡΒψΘΜ
ΔέΝ§œΏΘΚ«κΡψ”ΟΙβΜ§ΒΡ«ζœΏΥ≥¥ΈΝ§Ϋ”ΗςΒψΘ°

Θ®3Θ©άϊ”ΟΚ· ΐΆΦœσΫβΨωΘΚ
ΔΌΗΟΧ«ΙϊΚ–ΒΡΉν¥σ»ίΜΐ «__________ΘΜ
ΔΎ»τΗΟΧ«ΙϊΚ–ΒΡ»ίΜΐ≥§Ιΐ![]() Θ§«κΙάΦΤΧ«ΙϊΚ–ΒΡΒΉ±Ώ≥Λ
Θ§«κΙάΦΤΧ«ΙϊΚ–ΒΡΒΉ±Ώ≥Λ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°Θ®±ΘΝτ“ΜΈΜ–Γ ΐΘ©
ΒΡ»Γ÷ΒΖΕΈßΘ°Θ®±ΘΝτ“ΜΈΜ–Γ ΐΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫβ±Ψ–ΘΨ≈ΡξΦΕ―ß…ζΤΎΡ© ΐ―ßΩΦ ‘«ιΩωΘ§–ΓΝΝ‘ΎΨ≈ΡξΦΕΥφΜζ≥ι»ΓΝΥ“Μ≤ΩΖ÷―ß…ζΒΡΤΎΡ© ΐ―ß≥…Φ®ΈΣ―υ±ΨΘ§Ζ÷ΈΣ![]() Ζ÷)ΓΔ
Ζ÷)ΓΔ![]() Ζ÷)ΓΔ
Ζ÷)ΓΔ![]() Ζ÷)ΓΔ
Ζ÷)ΓΔ![]() Ζ÷)ΥΡΗωΒ»ΦΕΫχ––Ά≥ΦΤΘ§≤ΔΫΪΆ≥ΦΤΫαΙϊΜφ÷Τ≥…»γœ¬Ά≥ΦΤΆΦ±μΘ§«κΡψΗυΨίΆ≥ΦΤΆΦΫβ¥π“‘œ¬Έ ΧβΘΚ
Ζ÷)ΥΡΗωΒ»ΦΕΫχ––Ά≥ΦΤΘ§≤ΔΫΪΆ≥ΦΤΫαΙϊΜφ÷Τ≥…»γœ¬Ά≥ΦΤΆΦ±μΘ§«κΡψΗυΨίΆ≥ΦΤΆΦΫβ¥π“‘œ¬Έ ΧβΘΚ
Τδ÷–Ήι![]() ΒΡΤΎΡ© ΐ―ß≥…Φ®»γœ¬
ΒΡΤΎΡ© ΐ―ß≥…Φ®»γœ¬
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Θ®1Θ©«κ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®2Θ©’β≤ΩΖ÷―ß…ζΒΡΤΎΡ© ΐ―ß≥…Φ®ΒΡ÷–ΈΜ ΐ « Θ§![]() ΉιΒΡΤΎΡ© ΐ―ß≥…Φ®ΒΡ÷Ύ ΐ « ΘΜ
ΉιΒΡΤΎΡ© ΐ―ß≥…Φ®ΒΡ÷Ύ ΐ « ΘΜ
Θ®3Θ©’βΗω―ß–ΘΨ≈ΡξΦΕΙ≤”–―ß…ζ![]() »ΥΘ§»τΖ÷ ΐΈΣ
»ΥΘ§»τΖ÷ ΐΈΣ![]() Ζ÷(Κ§
Ζ÷(Κ§![]() Ζ÷)“‘…œΈΣ”≈–ψΘ§«κΙάΦΤ’β¥ΈΨ≈ΡξΦΕ―ß…ζΤΎΡ© ΐ―ßΩΦ ‘≥…Φ®ΈΣ”≈–ψΒΡ―ß…ζ»Υ ΐ¥σ‘Φ”–Εύ…ΌΘΩ
Ζ÷)“‘…œΈΣ”≈–ψΘ§«κΙάΦΤ’β¥ΈΨ≈ΡξΦΕ―ß…ζΤΎΡ© ΐ―ßΩΦ ‘≥…Φ®ΈΣ”≈–ψΒΡ―ß…ζ»Υ ΐ¥σ‘Φ”–Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫ––ΥΡ±Ώ–Έ![]() ÷–Θ§Βψ
÷–Θ§Βψ![]() ‘Ύ
‘Ύ![]() …œΘ§Ν§Ϋ”
…œΘ§Ν§Ϋ”![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() …œ“ΜΒψΘ§
…œ“ΜΒψΘ§![]() Θ°
Θ°
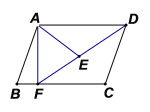
(1)«σ÷ΛΘΚ![]() ΓΉ
ΓΉ![]() ΘΜ
ΘΜ
(2)»τ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§«σ
Θ§«σ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ±Ώ≥ΛΈΣ5ΒΡΝβ–ΈABCD÷–Θ§Ε‘Ϋ«œΏAC≥ΛΈΣ6Θ§ΒψE‘ΎΕ‘Ϋ«œΏBD…œ«“tanΓœEAC=![]() Θ§‘ρBEΒΡ≥ΛΈΣ_____Θ°
Θ§‘ρBEΒΡ≥ΛΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®‘ΡΕΝάμΫβΘ©
Ϋη÷ζΆΦ–ΈΒΡ÷±Ιέ–‘Θ§Έ“Ο«Ω…“‘÷±Ϋ”ΒΟΒΫ“Μ–©”–Ιφ¬…ΒΡΥψ ΫΒΡΫαΙϊΘ§±»»γΘΚ”…ΆΦΔΌΘ§Ά®ΙΐΕ‘–ΓΚΎΒψΒΡΦΤ ΐΘ§Έ“Ο«Ω…“‘ΒΟΒΫ1+2+3+Γ≠+nΘΫ![]() nΘ®n+1Θ©ΘΜ”…ΆΦΔΎΘ§Ά®ΙΐΕ‘–Γ‘≤»ΠΒΡΦΤ ΐΘ§Έ“Ο«Ω…“‘ΒΟΒΫ1+3+5+Γ≠+Θ®2n©¹1Θ©ΘΫn2Θ°
nΘ®n+1Θ©ΘΜ”…ΆΦΔΎΘ§Ά®ΙΐΕ‘–Γ‘≤»ΠΒΡΦΤ ΐΘ§Έ“Ο«Ω…“‘ΒΟΒΫ1+3+5+Γ≠+Θ®2n©¹1Θ©ΘΫn2Θ°

Ρ«Ο¥13+23+33+Γ≠+n3ΫαΙϊΒ»”ΎΕύ…ΌΡΊΘΩ
»γΆΦΔέΘ§AB «’ΐΖΫ–ΈABCDΒΡ“Μ±ΏΘ§BBΓδΘΫnΘ§BΓδBΓεΘΫn©¹1Θ§BΓεBΓδΓδΓδΘΫn©¹2Θ§Γ≠Γ≠Θ§œ‘»ΜABΘΫ1+2+3+Γ≠+nΘΫ![]() nΘ®n+1Θ©Θ§Ζ÷±π“‘ABΓδΓΔABΓεΓΔABΓδΓδΓδΓΔΓ≠ΈΣ±ΏΉς’ΐΖΫ–ΈΘ§ΫΪ’ΐΖΫ–ΈABCDΖ÷Ην≥…ΩιΘ§ΟφΜΐΖ÷±πΦ«ΈΣSnΓΔSn©¹1ΓΔSn©¹2ΓΔΓ≠ΓΔS1Θ°
nΘ®n+1Θ©Θ§Ζ÷±π“‘ABΓδΓΔABΓεΓΔABΓδΓδΓδΓΔΓ≠ΈΣ±ΏΉς’ΐΖΫ–ΈΘ§ΫΪ’ΐΖΫ–ΈABCDΖ÷Ην≥…ΩιΘ§ΟφΜΐΖ÷±πΦ«ΈΣSnΓΔSn©¹1ΓΔSn©¹2ΓΔΓ≠ΓΔS1Θ°
Θ®Ιφ¬…ΧΫΨΩΘ©
ΫαΚœΆΦ–ΈΘ§Ω…“‘ΒΟΒΫSnΘΫ2BBΓδΓΝBC©¹BBΓδ2ΘΫΓΓ ΓΓΘ§
Ά§άμ”–Sn©¹1ΘΫΓΓ ΓΓΘ§Sn©¹2ΘΫΓΓ ΓΓΘ§Γ≠Θ§S1ΘΫ13Θ°
Υυ“‘13+23+33+Γ≠+n3ΘΫSΥΡ±Ώ–ΈABCDΘΫΓΓ ΓΓΘ°
Θ®ΫβΨωΈ ΧβΘ©
ΗυΨί“‘…œΖΔœ÷Θ§ΦΤΥψ![]() ΒΡΫαΙϊΈΣΓΓ ΓΓΘ°
ΒΡΫαΙϊΈΣΓΓ ΓΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ–¬ΙΎΉ¥≤ΓΕΨΒΡ”Αœλœ¬Θ§Ρ≥―ß–ΘΜΐΦΪœλ”Π’ΰΗ°Κ≈’ΌΘ§ΩΣ’ΙΝΥΓΑΆΘΩΈ≤ΜΆΘ―ßΓ±Άχ…œ ΎΩΈΙΛΉςΘ§ΈΣΝΥΆχ…œ ΎΩΈΙΛΉςΥ≥άϊΩΣ’ΙΚΆ»ΓΒΟΝΦΚΟ≥…–ßΘ§ΗΟ–Θ‘Ύ ΎΩΈΒΎ“Μ÷ήΚΆ ΎΩΈΒΎΕΰ÷ήΖ÷±πΥφΜζ≥ι»Γ≤ΩΖ÷―ß…ζΫχ––ΓΑΆχ…œ ΎΩΈΫΧ―ß–ßΙϊΖ¥άΓΓ±Άχ…œΒς≤ιΘ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§Βς≤ιœ‘ ΨΘΚΝΫ¥ΈΒς≤ιΖ¥άΓΫΧ―ß–ßΙϊΈΣΓΑΫœ≤νΓ±»Υ ΐœύΒ»Θ§ΒΎΕΰ÷ήΖ¥άΓΫΧ―ß–ßΙϊΈΣΓΑΚήΚΟΓ±»Υ ΐ±»άΐ±»ΒΎ“Μ÷ήΕύ![]() Θ§«κΗυΨίΒς≤ιœ‘ ΨΚΆΆ≥ΦΤΆΦ÷–ΒΡ–≈œΔΫβΨωœ¬Ν–Έ ΧβΘΚ
Θ§«κΗυΨίΒς≤ιœ‘ ΨΚΆΆ≥ΦΤΆΦ÷–ΒΡ–≈œΔΫβΨωœ¬Ν–Έ ΧβΘΚ
![]() ‘ΎΆΦ1÷–Θ§±μ ΨΓΑΫœΚΟΓ±ΒΡ…»–Έ‘≤–ΡΫ«
‘ΎΆΦ1÷–Θ§±μ ΨΓΑΫœΚΟΓ±ΒΡ…»–Έ‘≤–ΡΫ«![]() ΒΡΕ» ΐΈΣ_ Ε»Θ§≤ΔΑ―ΆΦ2Χθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
ΒΡΕ» ΐΈΣ_ Ε»Θ§≤ΔΑ―ΆΦ2Χθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
![]() »τΑ―Βς≤ιΖ¥άΓΫΧ―ß–ßΙϊΓΑΚήΚΟΓ±ΚΆΓΑΫœΚΟΓ±ΉςΈΣΆχ…œ ΎΩΈ≥…–ßΝΦΚΟΒΡ±ξΉΦΘ§ΗΟ–Θ¥σ‘Φ”–
»τΑ―Βς≤ιΖ¥άΓΫΧ―ß–ßΙϊΓΑΚήΚΟΓ±ΚΆΓΑΫœΚΟΓ±ΉςΈΣΆχ…œ ΎΩΈ≥…–ßΝΦΚΟΒΡ±ξΉΦΘ§ΗΟ–Θ¥σ‘Φ”–![]() Οϊ―ß…ζΘ§«κΙάΦΤ ΎΩΈΒΎΕΰ÷ή―ß–ΘΆχ…œ ΎΩΈ≥…–ßΝΦΚΟΒΡ―ß…ζ»Υ ΐΘΜ
Οϊ―ß…ζΘ§«κΙάΦΤ ΎΩΈΒΎΕΰ÷ή―ß–ΘΆχ…œ ΎΩΈ≥…–ßΝΦΚΟΒΡ―ß…ζ»Υ ΐΘΜ
![]() ”–“ΜΈΜΦ“≥Λ»œΈΣΘ§ΝΫ¥ΈΒς≤ιΖ¥άΓ ΎΩΈ–ßΙϊΈΣΓΑΫœ≤νΓ±»Υ ΐœύΒ»Θ§“ρ¥Υ―ß–Θ‘Ύ“Μ÷ήΚσΒς’ϊΒΡ¥κ ©≤ΔΟΜ”–ΧαΗΏΆχ…œ ΎΩΈ–ßΙϊΘ§’βΈΜΦ“≥ΛΖ÷Έω ΐΨίΒΡΖΫΖ®Κœάμ¬πΘΩ«κΫαΚœΆ≥ΦΤΆΦΘ§Ε‘’βΈΜΦ“≥ΛΖ÷Έω ΐΨίΒΡΖΫΖ®ΦΑ―ß–Θ‘Ύ“Μ÷ήΚσΒς’ϊ¥κ ©Ε‘Άχ…œ ΎΩΈ–ßΙϊΒΡ”ΑœλΧΗΧΗΡψΒΡΩ¥Ζ®Θ°
”–“ΜΈΜΦ“≥Λ»œΈΣΘ§ΝΫ¥ΈΒς≤ιΖ¥άΓ ΎΩΈ–ßΙϊΈΣΓΑΫœ≤νΓ±»Υ ΐœύΒ»Θ§“ρ¥Υ―ß–Θ‘Ύ“Μ÷ήΚσΒς’ϊΒΡ¥κ ©≤ΔΟΜ”–ΧαΗΏΆχ…œ ΎΩΈ–ßΙϊΘ§’βΈΜΦ“≥ΛΖ÷Έω ΐΨίΒΡΖΫΖ®Κœάμ¬πΘΩ«κΫαΚœΆ≥ΦΤΆΦΘ§Ε‘’βΈΜΦ“≥ΛΖ÷Έω ΐΨίΒΡΖΫΖ®ΦΑ―ß–Θ‘Ύ“Μ÷ήΚσΒς’ϊ¥κ ©Ε‘Άχ…œ ΎΩΈ–ßΙϊΒΡ”ΑœλΧΗΧΗΡψΒΡΩ¥Ζ®Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com