
【题目】如图,抛物线![]() 与
与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连结
,连结![]() ,点C(6,
,点C(6,![]() )在抛物线上,直线
)在抛物线上,直线![]() 与
与![]() 轴交于点
轴交于点![]()
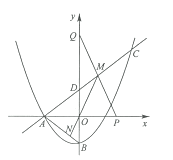
(1)求![]() 的值及直线
的值及直线![]() 的函数表达式;
的函数表达式;
(2)点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴正半轴上,连结
轴正半轴上,连结![]() 与直线
与直线![]() 交于点
交于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,若
,若![]() 为
为![]() 的中点.
的中点.
①求证:![]() ;
;
②设点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)c=-3; 直线AC的表达式为:y=![]() x+3;(2)①证明见解析;②
x+3;(2)①证明见解析;②![]()
【解析】
试题(1)把点C(6,![]() )代入
)代入![]() 中可求出c的值;令y=0,可得A点坐标,从而可确定AC的解析式;
中可求出c的值;令y=0,可得A点坐标,从而可确定AC的解析式;
(2)①分别求出tan∠OAB=tan∠OAD=![]() ,得∠OAB=tan∠OAD,再由M就PQ的中点,得OM=MP,所以可证得∠APM=∠AON,即可证明
,得∠OAB=tan∠OAD,再由M就PQ的中点,得OM=MP,所以可证得∠APM=∠AON,即可证明![]() ;
;
②过M点作ME⊥x轴,垂足为E,分别用含有m的代数式表示出AE和AM的长,然后利用![]() 即可求解.
即可求解.
试题(1)把点C(6,![]() )代入
)代入![]()
解得:c=-3
∴![]()
当y=0时,![]()
解得:x1=-4,x2=3
∴A(-4,0)
设直线AC的表达式为:y=kx+b(k≠0)
把A(-4,0),C(6,![]() )代入得
)代入得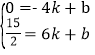
解得:k=![]() ,b=3
,b=3
∴直线AC的表达式为:y=![]() x+3
x+3
(2)①在RtΔAOB中,tan∠OAB=![]()
在RtΔAOD中,tan∠OAD=![]()
∴∠OAB=∠OAD
∵在RtΔPOQ中,M为PQ的中点
∴OM=MP
∴∠MOP=∠MPO
∵∠MPO=∠AON
∴∠APM=∠AON
∴ΔAPM∽ΔAON
②如图,过点M作ME⊥x轴于点E
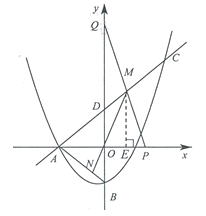
又∵OM=MP
∴OE=EP
∵点M横坐标为m
∴AE=m+4 AP=2m+4
∵tan∠OAD=![]()
∴cos∠EAM=cos∠OAD=![]()
∴AM=![]() AE=
AE=![]()
∵ΔAPM∽ΔAON
∴![]()
∴AN=![]()


科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在一个点M,使得MP=MC,则称点P为⊙C的“等径点”,已知点D(![]() ,
,![]() ),E(0,2
),E(0,2![]() ),F(﹣2,0).
),F(﹣2,0).
(1)当⊙O的半径为1时,
①在点D,E,F中,⊙O的“等径点”是哪几个点;
②作直线EF,若直线EF上的点T(m,n)是⊙O的“等径点”,求m的取值范围.
(2)过点E作EG⊥EF交x轴于点G,若△EFG各边上所有的点都是某个圆的“等径点”,求这个圆的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
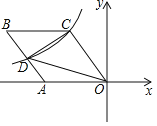
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米,垂直于地面放置的标杆在地面上的影长为2米,则树的高度为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
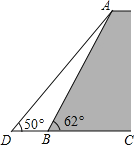
【题目】如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),点
的左侧),点![]() 的坐标为
的坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() .动点
.动点![]() 在
在![]() 轴上运动,过点
轴上运动,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
(Ⅰ)求抛物线的解析式和直线![]() 的解析式;
的解析式;
(Ⅱ)当点![]() 在线段
在线段![]() 上运动时,求线段
上运动时,求线段![]() 的最大值;
的最大值;
(Ⅲ)当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,直接写出
为顶点的四边形是平行四边形时,直接写出![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com