
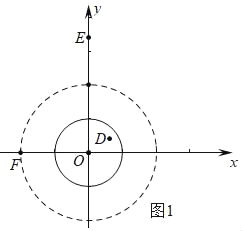
ЁОЬтФПЁПЖдгкЦНУцжБНЧзјБъЯЕxOyжаЕФЕуPКЭЁбCЃЌИјГіШчЯТЖЈвхЃКШєЁбCЩЯДцдквЛИіЕуMЃЌЪЙЕУMPЃНMCЃЌдђГЦЕуPЮЊЁбCЕФЁАЕШОЖЕуЁБЃЌвбжЊЕуDЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌEЃЈ0ЃЌ2
ЃЉЃЌEЃЈ0ЃЌ2![]() ЃЉЃЌFЃЈЉ2ЃЌ0ЃЉЃЎ
ЃЉЃЌFЃЈЉ2ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЕБЁбOЕФАыОЖЮЊ1ЪБЃЌ
ЂйдкЕуDЃЌEЃЌFжаЃЌЁбOЕФЁАЕШОЖЕуЁБЪЧФФМИИіЕуЃЛ
ЂкзїжБЯпEFЃЌШєжБЯпEFЩЯЕФЕуTЃЈmЃЌnЃЉЪЧЁбOЕФЁАЕШОЖЕуЁБЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉЙ§ЕуEзїEGЁЭEFНЛxжсгкЕуGЃЌШєЁїEFGИїБпЩЯЫљгаЕФЕуЖМЪЧФГИідВЕФЁАЕШОЖЕуЁБЃЌЧѓетИідВЕФАыОЖrЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйЁбOЕФЁАЕШОЖЕуЁБЪЧDЃЌEЃЛЂкЉ2ЁмmЁмЉ1ЃЛЃЈ2ЃЉетИідВЕФАыОЖrЕФШЁжЕЗЖЮЇЮЊrЁн2ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОнЁАЕШОЖЕуЁБЕФЖЈвхПЩжЊЃЌЁАЕШОЖЕуЁБЕНдВаФЕФОрРыаЁгкЕШгкдВЕФАыОЖЕФ2БЖЃЌгЩДЫМДПЩХаЖЈЃЛ
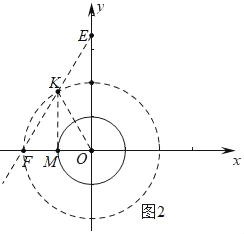
ЂкШчЭМ2жаЃЌЩшжБЯпEFНЛАыОЖЮЊ2ЕФЁбOгкЕуKЃЌСЌНгOKЃЌзїKMЁЭOFгкMЃЎЕБЕуTдкЯпЖЮFKЩЯЪБЃЌЕуTЪЧЁАЕШОЖЕуЁБЃЌЧѓГіЕуKЕФзјБъМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉвђЮЊЁїEFGИїБпЩЯЫљгаЕФЕуЖМЪЧФГИідВЕФЁАЕШОЖЕуЁБЃЌЫљвдетИідВЕФдВаФQЪЧЯпЖЮFGЕФжаЕуЃЌвзжЊQЃЈ2ЃЌ0ЃЉЃЌЩшетИідВЕФАыОЖЮЊrЃЎИљОнQGЁм2rЃЌЙЙНЈВЛЕШЪНМДПЩНтОіЮЪЬт.
ЃЈ1ЃЉИљОнЁАЕШОЖЕуЁБЕФЖЈвхПЩжЊЃЌЁАЕШОЖЕуЁБЕНдВаФЕФОрРыаЁгкЕШгкдВЕФАыОЖЕФ2БЖЃЎМДАыОЖЮЊ1ЕФЁбOЕФЁАЕШОЖЕуЁБдквдOЮЊдВаФ2ЮЊАыОЖЕФдВФкЛђдВЩЯЃЎ
ШчЭМ1жаЃЌЙлВьЭМЯѓПЩжЊЃКдкЕуDЃЌEЃЌFжаЃЌЁбOЕФЁАЕШОЖЕуЁБЪЧDЃЌEЃЎ
ЂкШчЭМ2жаЃЌЩшжБЯпEFНЛАыОЖЮЊ2ЕФЁбOгкЕуKЃЌСЌНгOKЃЌзїKMЁЭOFгкMЃЎ
ЁпOFЃН2ЃЌOEЃН2![]() ЃЌ
ЃЌ
ЁрtanЁЯEFOЃН![]() =
=![]() ЃЌ
ЃЌ
ЁрЁЯOFKЃН60ЁуЃЌ
ЁпOFЃНOKЃЌ
ЁрЁїOFKЪЧЕШБпШ§НЧаЮЃЌ
ЁрOFЃНOKЃНFKЃН2ЃЌ
ЁпKMЁЭOFЃЌ
ЁрFMЃНOMЃН1ЃЌKMЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрKЃЈЉ1ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпЕБЕуTдкЯпЖЮFKЩЯЪБЃЌЕуTЪЧЁАЕШОЖЕуЁБЃЌ
ЁрЉ2ЁмmЁмЉ1ЃЎ
ЃЈ2ЃЉШчЭМ3жаЃЌ
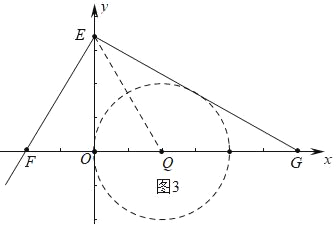
ЁпЁїEFGЪЧжБНЧШ§НЧаЮЃЌЁЯFEGЃН90ЁуЃЌЁЯEFGЃН60ЁуЃЌ
ЁрEFЃН2OFЃН4ЃЌFGЃН2EFЃН8ЃЌ
ЁрOGЃН6ЃЌ
гЩЬтвтЁїEFGИїБпЩЯЫљгаЕФЕуЖМЪЧФГИідВЕФЁАЕШОЖЕуЁБЃЌетИідВЕФдВаФQЪЧЯпЖЮFGЕФжаЕуЃЌQЃЈ2ЃЌ0ЃЉЃЌЩшетИідВЕФАыОЖЮЊrЃЎ
гЩЬтвтЃКQGЁм2r
Ёр4Ём2rЃЌ
ЁрrЁн2ЃЌ
МДетИідВЕФАыОЖrЕФШЁжЕЗЖЮЇЮЊrЁн2ЃЎ


 ПьРж5Мг2Н№ОэЯЕСаД№АИ
ПьРж5Мг2Н№ОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдке§ЗНаЮABCDжаЃЌGЮЊCDБпжаЕуЃЌСЌНгAGВЂбгГЄНЛBCБпЕФбгГЄЯпгкEЕуЃЌЖдНЧЯпBDНЛAGгкFЕуЃЎвбжЊFG=2ЃЌдђЯпЖЮAEЕФГЄЖШЮЊЃЈЁЁЁЁЃЉ
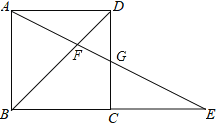
A. 6 B. 8 C. 10 D. 12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЖўДЮКЏЪ§y=ax2+bx+cЕФЭМЯѓПЊПкЯђЩЯЃЌЭМЯѓОЙ§ЕуЃЈЉ1ЃЌ2ЃЉКЭЃЈ1ЃЌ0ЃЉЃЌЧвгыyжсНЛгкИКАыжсЃЌИјГіСљИіНсТлЃКЂйaЃО0ЃЛЂкbЃО0ЃЛЂлcЃО0ЃЛЂмa+b+c=0ЃЛЂнb2Љ4acЃО0ЃЛЂо2aЉbЃО0ЃЌЦфжае§ШЗНсТлађКХЪЧ_____ЃЎ
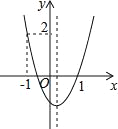
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСѕсчЪЧЮвЙњЙХДњзюНмГіЕФЪ§бЇМвжЎвЛЃЌЫћдкЁЖОХЫуЪѕдВЬяЪѕЃЉжагУЁАИюдВЪѕЁБжЄУїСЫдВУцЛ§ЕФОЋШЗЙЋЪНЃЌВЂИјГіСЫМЦЫудВжмТЪЕФПЦбЇЗНЗЈЃЈзЂЃКдВжмТЪЃНдВЕФжмГЄгыИУдВжБОЖЕФБШжЕЃЉЁАИюдВЪѕЁБОЭЪЧвдЁАдВФкНге§ЖрБпаЮЕФУцЛ§ЁБЃЌРДЮоЯоБЦНќЁАдВУцЛ§ЁБЃЌСѕЛеаЮШнЫћЕФЁАИюдВЪѕЁБЫЕЃКИюжЎУжЯИЃЌЫљЪЇУжЩйЃЌИюжЎгжИюЃЌвджСгкВЛПЩИюЃЌдђгыдВКЯЬхЃЌЖјЮоЫљЪЇвгЃЎСѕЛеМЦЫудВжмТЪЪЧДге§СљБпаЮПЊЪМЕФЃЌвзжЊдВЕФФкНге§СљБпаЮПЩЗжЮЊСљИіШЋЕШЕФе§Ш§НЧаЮЃЌУПИіШ§НЧаЮЕФБпГЄОљЮЊдВЕФАыОЖRЃЎДЫЪБдВФкНге§СљБпаЮЕФжмГЄЮЊ6RЃЌШчЙћНЋдВФкНге§СљБпаЮЕФжмГЄЕШЭЌгкдВЕФжмГЄЃЌПЩЕУдВжмТЪЮЊ3ЃЎЕБе§ЪЎЖўБпаЮФкНггкдВЪБЃЌШчЙћАДееЩЯЪіЗНЗЈМЦЫуЃЌПЩЕУдВжмТЪЮЊ_____ЃЎЃЈВЮПМЪ§ОнЃКsinl5ЁуЃН0.26ЃЉ
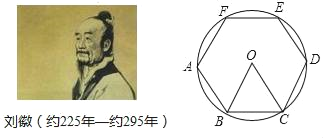
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁемЕФЙУТшОгЊвЛМвЛЈЕъЃЌЫцзХдНРДдНЖрЕФШЫЯВАЎЁАЖрШтжВЮяЁБЃЌЙУТшвВДђЫуЯњЪлЁАЖрШтжВЮяЁБЃЎаЁемАяжњЙУТшеыЖдФГжжЁАЖрШтжВЮяЁБзіСЫЪаГЁЕїВщКѓЃЌЛцжЦСЫвдЯТСНеХЭМБэЃК
ЃЈ1ЃЉШчЙћдкШ§дТЗнГіЪлетжжжВЮяЃЌЕЅжъЛёРћЖрЩйдЊЃЛ
ЃЈ2ЃЉЧыФудЫгУЫљбЇжЊЪЖЃЌАяжњЙУТшЧѓГідкФФИідТЯњЪлетжжЖрШтжВЮяЃЌЕЅжъЛёРћзюДѓЃПЃЈЬсЪОЃКЕЅжъЛёРћЃНЕЅжъЪлМлЉЕЅжъГЩБОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтЃКЂйЫљгаШёНЧШ§НЧКЏЪ§жЕЖМЮЊе§Ъ§ЃЛЂкНтжБНЧШ§НЧаЮЪБжЛашвбжЊГ§жБНЧЭтЕФСНИідЊЫиЃЛЂлRtЁїABCжаЃЌЁЯB=90ЁуЃЌдђsin2A+cos2A=1ЃЛЂмRtЁїABCжаЃЌЁЯA=90ЁуЃЌдђtanCsinC=cosCЃЎЦфжае§ШЗЕФУќЬтгаЃЈЁЁЁЁЃЉ
A. 0Иі B. 1Иі C. 2Иі D. 3Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсЕФИКАыжсНЛгкЕу
жсЕФИКАыжсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌЕуC(6ЃЌ
ЃЌЕуC(6ЃЌ![]() )дкХзЮяЯпЩЯЃЌжБЯп
)дкХзЮяЯпЩЯЃЌжБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]()
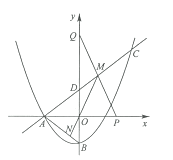
(1)Чѓ![]() ЕФжЕМАжБЯп
ЕФжЕМАжБЯп![]() ЕФКЏЪ§БэДяЪНЃЛ
ЕФКЏЪ§БэДяЪНЃЛ
(2)Еу![]() дк
дк![]() жсе§АыжсЩЯЃЌЕу
жсе§АыжсЩЯЃЌЕу![]() дк
дк![]() жсе§АыжсЩЯЃЌСЌНс
жсе§АыжсЩЯЃЌСЌНс![]() гыжБЯп
гыжБЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
ЂйЧѓжЄЃК![]() ЃЛ
ЃЛ
ЂкЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ(гУКЌ
ЕФГЄ(гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЎ
ЕФДњЪ§ЪНБэЪО)ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЬЪвРяЕФвћЫЎЛњНгЭЈЕчдДОЭНјШыздЖЏГЬађЃЌПЊЛњМгШШЪБУПЗжжгЩЯЩ§10ЁцЃЌМгШШЕН100ЁцЃЌЭЃжЙМгШШЃЌЫЎЮТПЊЪМЯТНЕЃЌДЫЪБЫЎЮТЃЈЁцЃЉгыПЊЛњКѓгУЪБЃЈminЃЉГЩЗДБШР§ЙиЯЕЃЎжБжСЫЎЮТНЕжС30ЁцЃЌвћЫЎЛњЙиЛњЃЎвћЫЎЛњЙиЛњКѓМДПЬздЖЏПЊЛњЃЌжиИДЩЯЪіздЖЏГЬађЃЎШєдкЫЎЮТЮЊ30ЁцЪБЃЌНгЭЈЕчдДКѓЃЌЫЎЮТyЃЈЁцЃЉКЭЪБМфЃЈminЃЉЕФЙиЯЕШчЭМЃЌЮЊСЫдкЩЯЮчЕквЛНкЯТПЮЪБЃЈ8ЃК45ЃЉФмКШЕНВЛГЌЙ§50ЁцЕФЫЎЃЌдђНгЭЈЕчдДЕФЪБМфПЩвдЪЧЕБЬьЩЯЮчЕФ
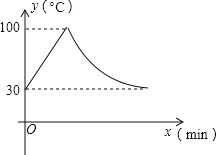
AЃЎ7ЃК20 BЃЎ7ЃК30 CЃЎ7ЃК45 DЃЎ7ЃК50
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
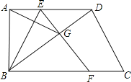
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЕу
ЃЎЕу![]() ЮЊБп
ЮЊБп![]() ЩЯвЛЕуЃЌНЋ
ЩЯвЛЕуЃЌНЋ![]() бижБЯп
бижБЯп![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() ТфдкЫФБпаЮЖдНЧЯп
ТфдкЫФБпаЮЖдНЧЯп![]() ЩЯЕФЕу
ЩЯЕФЕу![]() ДІЃЌ
ДІЃЌ![]() ЕФбгГЄЯпНЛжБЯп
ЕФбгГЄЯпНЛжБЯп![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
![]() Еу
Еу![]() ПЩвдЪЧ
ПЩвдЪЧ![]() ЕФжаЕуТ№ЃПЧыЫЕУїРэгЩЃЛ
ЕФжаЕуТ№ЃПЧыЫЕУїРэгЩЃЛ
![]() ЧѓжЄЃК
ЧѓжЄЃК![]() ЃЛ
ЃЛ
![]() Щш
Щш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЕБЫФБпаЮ
ЃЎЕБЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЪБЃЌЧѓ
ЮЊЦНааЫФБпаЮЪБЃЌЧѓ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() гІТњзуЕФЙиЯЕЃЎ
гІТњзуЕФЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com