
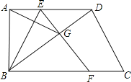
【题目】已知:如图,在四边形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为边
为边![]() 上一点,将
上一点,将![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在四边形对角线
落在四边形对角线![]() 上的点
上的点![]() 处,
处,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .
.
![]() 点
点![]() 可以是
可以是![]() 的中点吗?请说明理由;
的中点吗?请说明理由;
![]() 求证:
求证:![]() ;
;
![]() 设
设![]() ,
,![]() ,
,![]() .当四边形
.当四边形![]() 为平行四边形时,求
为平行四边形时,求![]() ,
,![]() ,
,![]() 应满足的关系.
应满足的关系.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在一个点M,使得MP=MC,则称点P为⊙C的“等径点”,已知点D(![]() ,
,![]() ),E(0,2
),E(0,2![]() ),F(﹣2,0).
),F(﹣2,0).
(1)当⊙O的半径为1时,
①在点D,E,F中,⊙O的“等径点”是哪几个点;
②作直线EF,若直线EF上的点T(m,n)是⊙O的“等径点”,求m的取值范围.
(2)过点E作EG⊥EF交x轴于点G,若△EFG各边上所有的点都是某个圆的“等径点”,求这个圆的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
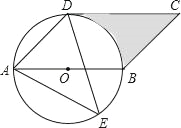
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)试判断CD与⊙O的位置关系,并说明理由.
(2)若BC=2.求阴影部分的面积.(结果保留π的形式)
查看答案和解析>>
科目:初中数学 来源: 题型:
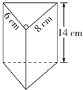
【题目】小亮要利用废纸板做一个三棱柱形状的无盖的笔筒,设计三棱柱的立体模型如图所示.
(1)请画出该立体模型的三视图;
(2)该笔筒至少要用多少废纸板?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八届五中全会出台了全面实施一对夫妇可生育两个孩子的政策,这是党中央站在中华民族长远发展的战略高度作出的促进人口长期均衡发展的重大举措. 二孩政策出台后,某家庭积极响应政府号召,准备生育两个小孩(假设生男生女机会均等,且与顺序无关).
(1)该家庭生育两胎,假设每胎都生育一个小孩,求这两个小孩恰好都是女孩的概率;
(2)该家庭生育两胎,假设第一胎生育一个小孩,且第二胎生育一对双胞胎,求这三个小孩中恰好是2女1男的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),点
的左侧),点![]() 的坐标为
的坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() .动点
.动点![]() 在
在![]() 轴上运动,过点
轴上运动,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
(Ⅰ)求抛物线的解析式和直线![]() 的解析式;
的解析式;
(Ⅱ)当点![]() 在线段
在线段![]() 上运动时,求线段
上运动时,求线段![]() 的最大值;
的最大值;
(Ⅲ)当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,直接写出
为顶点的四边形是平行四边形时,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
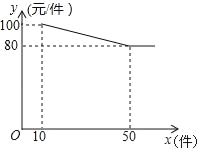
【题目】服装厂批发某种服装,每件成本为65元,规定不低于10件可以批发,其批发价y(元/件)与批发数量x(件)(x为正整数)之间所满足的函数关系如图所示.
(1)求y与x之间所满足的函数关系式,并写出x的取值范围;
(2)设服装厂所获利润为w(元),若10≤x≤50(x为正整数),求批发该种服装多少件时,服装厂获得利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
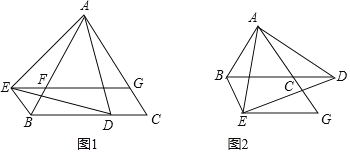
【题目】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,交射线AC于点G,连接BE.
(1)如图1所示,当点D在线段BC上时,求证:四边形BCGE是平行四边形;
(2)如图2所示,当点D在BC的延长线上时,(1)中的结论是否成立?并请说明理由;
(3)当点D运动到什么位置时,四边形BCGE是菱形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com