
����Ŀ�����¹�״������Ӱ���£�ijѧУ������Ӧ�������٣���չ�ˡ�ͣ�β�ͣѧ�������ڿι�����Ϊ�������ڿι���˳����չ��ȡ�����ó�Ч����У���ڿε�һ�ܺ��ڿεڶ��ֱܷ������ȡ����ѧ�����С������ڿν�ѧЧ�����������ϵ��飬�������������Ƴ�����������������ͳ��ͼ��������ʾ�����ε��鷴����ѧЧ��Ϊ���ϲ������ȣ��ڶ��ܷ�����ѧЧ��Ϊ���ܺá����������ȵ�һ�ܶ�![]() ������ݵ�����ʾ��ͳ��ͼ�е���Ϣ����������⣺
������ݵ�����ʾ��ͳ��ͼ�е���Ϣ����������⣺
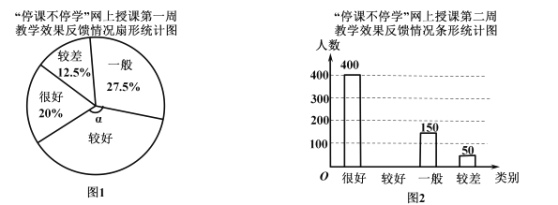
![]() ��ͼ1�У���ʾ���Ϻá�������Բ�Ľ�
��ͼ1�У���ʾ���Ϻá�������Բ�Ľ�![]() �Ķ���Ϊ_ �ȣ�����ͼ2����ͳ��ͼ����������
�Ķ���Ϊ_ �ȣ�����ͼ2����ͳ��ͼ����������
![]() ���ѵ��鷴����ѧЧ�����ܺá��͡��Ϻá���Ϊ�����ڿγ�Ч���õı�����У��Լ��
���ѵ��鷴����ѧЧ�����ܺá��͡��Ϻá���Ϊ�����ڿγ�Ч���õı�����У��Լ��![]() ��ѧ����������ڿεڶ���ѧУ�����ڿγ�Ч���õ�ѧ��������
��ѧ����������ڿεڶ���ѧУ�����ڿγ�Ч���õ�ѧ��������
![]() ��һλ�ҳ���Ϊ�����ε��鷴���ڿ�Ч��Ϊ���ϲ���������ȣ����ѧУ��һ�ܺ�����Ĵ�ʩ��û����������ڿ�Ч������λ�ҳ��������ݵķ�������������ͳ��ͼ������λ�ҳ��������ݵķ�����ѧУ��һ�ܺ������ʩ�������ڿ�Ч����Ӱ��̸̸��Ŀ�����
��һλ�ҳ���Ϊ�����ε��鷴���ڿ�Ч��Ϊ���ϲ���������ȣ����ѧУ��һ�ܺ�����Ĵ�ʩ��û����������ڿ�Ч������λ�ҳ��������ݵķ�������������ͳ��ͼ������λ�ҳ��������ݵķ�����ѧУ��һ�ܺ������ʩ�������ڿ�Ч����Ӱ��̸̸��Ŀ�����
���𰸡���1��144����ȫͼ�μ���������2��2000�ˣ���3���ҳ��������ݵķ���������������������
��������
��1�����ݰٷֱ�֮�͵���1��⼴�ɣ�
��2������![]() Ч�����õİٷ��ʼ��㼴�ɣ�
Ч�����õİٷ��ʼ��㼴�ɣ�
��3�������������������˼�������⼴�ɣ�
�⣺��1����ʾ���Ϻá�������Բ�Ľ�![]() �Ķ���
�Ķ���![]()
�ʴ�Ϊ144��
�ߵڶ��ܷ�����ѧЧ��Ϊ���ܺ������������ȵ�һ�ܶ�![]() ��
��
��ڶ�����������Ϊ400�£�20%+20%��=1000��
��ڶ��ܷ�����ѧЧ��Ϊ���Ϻ�������Ϊ1000-400-150-50=400���ˣ���
����ͳ��ͼ������ͼ��
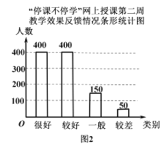
��2��![]() ����
����![]() ��
��
���ڿεڶ���ѧУ�����ڿγ�Ч���õ�ѧ������ԼΪ1500�ˣ�
��3���ҳ��������ݵķ�����������
��Ȼ���ε��鷴����ѧЧ��Ϊ���ϲ������ȣ������ε��������������ͬ��
���ҵڶ��ܷ�����ѧЧ��Ϊ���ܺá����������ȵ�һ�ܶ�![]() �������������Ե�����ʩ�������ڿ�Ч������ߣ�
�������������Ե�����ʩ�������ڿ�Ч������ߣ�


 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
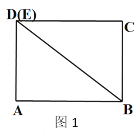
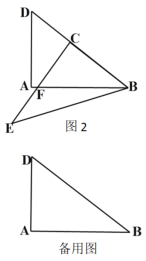
����Ŀ�����ۺ���ʵ�����ϣ���ʦ��֯ͬѧ������������ֽƬ����ת��Ϊ���չ��ѧ�����ͼ1�����о���ֽƬABCD��AB��8cm��AD��6cm������BD��������ABCD��BD�������õ���ABD�͡�BCE�����֡�ABDλ�ò��䣬����BCE��ͼ1��λ�ÿ�ʼ���Ƶ�B����ʱ�뷽����ת����ת��Ϊ����0��ܦ���360�������ڡ�BCE��ת�����У���CE���AB���ڵ�F��
��1����ͼ2����ͼ1�еġ�BCE��ת����C���ڱ�BD��ʱ��CF= ��
��2��������ת��BCE������E����DA�ӳ�����ʱ�����CF�ij���
��3���ڡ�BCE��ת�����У�����AE��AC����AC��AEʱ��ֱ��д����ʱ���Ķ�������AEC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У��Խ���AC��BD���ڵ�O��BD��6cm��AD��8cm��AB��10cm����E�ӵ�B��������BA���������˶����ٶ�Ϊ1cm/s��ͬʱ����G�ӵ�C��������CB���������˶����ٶ�Ϊ2cm/s����һ����ֹͣ�˶�ʱ����һ����Ҳֹͣ�˶�������OE������G��GF��BD�����˶�ʱ��Ϊt��s����0��t��4��������������⣺
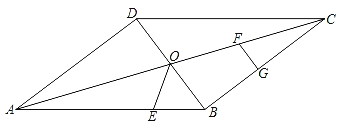
��1����tΪ��ֵʱ����BOE�ǵ��������Σ�
��2���������OEBGF���ΪS����ȷ��S��t�ĺ�����ϵʽ��
��3�����˶������У��Ƿ����ijһʱ��t��ʹS�����OEBGF��S��ACD��19��40�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��4�����˶������У��Ƿ����ijһʱ��t��ʹ��OBƽ�֡�COE�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
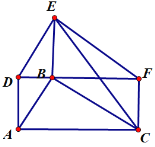
����Ŀ����ͼ����DEF�ɡ�ABCƽ�Ƶõ�����DFE=��CDF=30������DEF=90����BE��DF�ڵ�B������CE��AB=3��
��1����֤���ı���ACDFΪ����
��2�����߶�CE�ij��͡�CEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ����
����![]() ���߶�
���߶�![]() �ϣ�
�ϣ�![]() ��ֱ��
��ֱ��![]() ��һ�㣮
��һ�㣮
(1)��ͼ1����![]() ����
����![]() ��
��![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() ����֤��
����֤��![]() ��
��
(2)��ͼ2����![]() ����
����![]() ��
��![]() ���е㣬��
���е㣬��![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ��
��![]() �ϵ�һ������(��
�ϵ�һ������(��![]() ���
���![]() ��
��![]() ���غ�)������
���غ�)������![]() �Ķ���
�Ķ���![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ�̽��
�ϣ�̽��![]() ��
��![]() �Ĺ�ϵ��������֤����
�Ĺ�ϵ��������֤����
(3)��(2)�������£�����![]() ����ʲô����ʱ���߶�
����ʲô����ʱ���߶�![]() �ij����?(ֱ�Ӹ������ۣ�����˵������)
�ij����?(ֱ�Ӹ������ۣ�����˵������)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ������ÿ��
������ÿ��![]() ����λ���ȵ��ٶ����յ�
����λ���ȵ��ٶ����յ�![]() �˶�����
�˶�����![]() ����
����![]() �غϣ�������
�غϣ�������![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ��
��![]() ��������������
��������������![]() ��
��![]() ���ڱ�
���ڱ�![]() �����
�����![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() ���룩��
���룩��

��1��ֱ���ú�![]() �Ĵ���ʽ��ʾ�߶�
�Ĵ���ʽ��ʾ�߶�![]() �ij���
�ij���
��2������![]() ���ڱ�
���ڱ�![]() ��ʱ����
��ʱ����![]() ��ֵ��
��ֵ��
��3����������![]() ��
��![]() �ص�����ͼ��Ϊ�ı���ʱ�����ı��ε����Ϊ
�ص�����ͼ��Ϊ�ı���ʱ�����ı��ε����Ϊ![]() ��ƽ����λ������
��ƽ����λ������![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��4����![]() ��
Ϊ��![]() ���е㣬ֱ��д��ֱ��
���е㣬ֱ��д��ֱ��![]() ��������
��������![]() �ֳɵ�������ͼ�ε������Ϊ
�ֳɵ�������ͼ�ε������Ϊ![]() ʱ
ʱ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
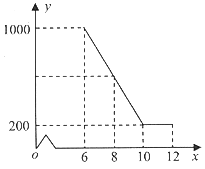
����Ŀ��ijפ���ƶС��ʵʩ��ҵ��ƶ������ƶ��ũ������������ֲ������.��֪���ϵijɱ�Ϊ6Ԫ/ǧ�ˣ��涨���۵��۲����ڳɱ����ֲ����ڳɱ�������.�����г����鷢�֣�ij�����ϵ�������y(ǧ��)�����۵���x(Ԫ/ǧ��)�ĺ�����ϵ����ͼ��ʾ��
(1)��y��x�ĺ�������ʽ(Ҳ�ƹ�ϵʽ)��
(2)����һ���������ϻ�õ���������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����EΪ�߶�BO��һ�㣬����CE����CE�Ƶ�C˳ʱ����ת90��õ�CF������EF��CD�ڵ�G��
��1����AB��4��BE��![]() �����CEF�������
�����CEF�������
��2����ͼ2���߶�FE���ӳ��߽�AB�ڵ�H������F��FM��CD�ڵ�M����֤��BH+MG��![]() BE��
BE��
��3����ͼ3����EΪ����OD��һ�㣬�߶�FE���ӳ��߽�ֱ��CD�ڵ�G����ֱ��AB�ڵ�H������F��FM��ֱֱ��CD�ڵ�M����ֱ��д���߶�BH��MG��BE��������ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
����һ�����Լ����ָ���������������е�Լ��������һ�������ǽ���������a��b�����Լ����ʾΪ(a��b)����(12��18)=6��(7��9)=1��
���϶�����7x+3y=11��һ�������⣬��Ҫ��Ϊ�������裺
��һ������x��ʾy����y![]() ��
��
�ڶ�������һ������x��ʹ��11��7x��3�ı�����Ϊ�������ҵ�������x����11��7x����Ϊ12��9x+2x��1=3(4��3x)+2x��1����ֻ��2x��1��3�ı������ɣ�Ϊ�˿�ȡx=2��
����������x=2����y![]() ����y=��1����
����y=��1����![]() ��ԭ���̵�һ�������⣮
��ԭ���̵�һ�������⣮
��������������x��y�Ķ�Ԫһ�η���ax+by=c(a��b��c��Ϊ����)��������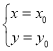 ������������������Ϊ
������������������Ϊ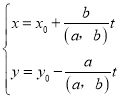 (tΪ����)��
(t����)��
�������ϲ��ϣ�����������⣺
��1����(15��20)x+(4��8)y=99��һ�������⣻
��2����(15��20)x+(4��8)y=99�м����������⣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com