
【题目】如图,在Rt△ABC中,∠ACB = 90,D为AB的中点,AE∥DC,CE∥DA.
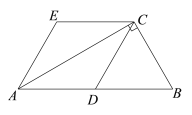
(1)求证:四边形ADCE是菱形;
(2)连接DE,若AC =![]() ,BC =2,求证:△ADE是等边三角形.
,BC =2,求证:△ADE是等边三角形.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)先根据题意证明四边形ADCE是平行四边形,再由直角三角形斜边中线等于斜边的一半可得AD= BD=CD,即可可求证结论;
(2)在Rt△ABC中,由三角函数值可知∠CAB=30,继而根据菱形的性质可知AE = AD,∠EAD=2∠CAB=60,进而即可求证结论.
证明:(1)∵ AE∥DC,CE∥DA,
∴ 四边形ADCE是平行四边形.
∵ 在Rt△ABC中, D为AB的中点,
∴ AD= BD=CD=![]() .
.
∴ 四边形ADCE是菱形.
(2)在Rt△ABC中,AC =![]() ,BC =2,
,BC =2,
∴ ![]() .
.
∴ ∠CAB=30.
∵ 四边形ADCE是菱形.
∴ AE = AD,∠EAD=2∠CAB=60.
∴ △ADE是等边三角形.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.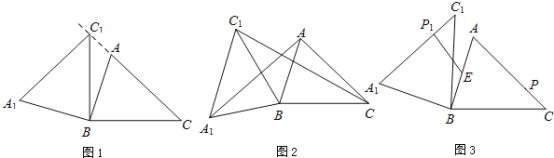
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,楼顶有一根天线,为了测量楼的高度,在地面上取成一条直线的三点E、D、C,在点C处测得天线顶端A的仰角为60°,从点C走到点D,CD=6米,从点D处测得天线下端B的仰角为45°.又知A、B、E在一条线上,AB=25米,求楼高BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连结
,连结![]() ,点C(6,
,点C(6,![]() )在抛物线上,直线
)在抛物线上,直线![]() 与
与![]() 轴交于点
轴交于点![]()
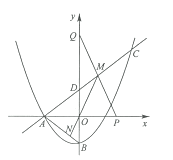
(1)求![]() 的值及直线
的值及直线![]() 的函数表达式;
的函数表达式;
(2)点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴正半轴上,连结
轴正半轴上,连结![]() 与直线
与直线![]() 交于点
交于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,若
,若![]() 为
为![]() 的中点.
的中点.
①求证:![]() ;
;
②设点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
(1)当![]() 时,
时,
①写出抛物线的对称轴;
②求抛物线的表达式;
(2)存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90,D为AB的中点,AE∥DC,CE∥DA.
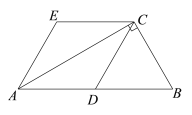
(1)求证:四边形ADCE是菱形;
(2)连接DE,若AC =![]() ,BC =2,求证:△ADE是等边三角形.
,BC =2,求证:△ADE是等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com