
【题目】已知:如图,楼顶有一根天线,为了测量楼的高度,在地面上取成一条直线的三点E、D、C,在点C处测得天线顶端A的仰角为60°,从点C走到点D,CD=6米,从点D处测得天线下端B的仰角为45°.又知A、B、E在一条线上,AB=25米,求楼高BE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤![]() .其中正确的个数为( ).
.其中正确的个数为( ).
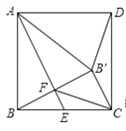
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元作为固定投资,已知生产每件产品的成本是40元.在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利(年获利=年销售额一生产成本—投资)为z(万元).
(1)试写出y与x之间的函数关系式(不写x的取值范围);
(2)试写出z与x之间的函数关系式(不写x的取值范围);
(3)公司计划,在第一年按年获利最大确定销售单价进行销售;到第二年年底获利不低于1130万元,请借助函数的大致图象说明:第二年的销售单价x(元)应确定在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上(不与
上(不与![]() 重合),将矩形沿
重合),将矩形沿![]() 折叠,使点
折叠,使点![]() 分别落在点
分别落在点![]() 处有下列结论:
处有下列结论:
①![]() 与
与![]() 互余;
互余;
②若![]() 平分
平分![]() 则
则![]()
③若直线![]() 经过点
经过点![]() 则
则![]()
④若直线![]() 交边
交边![]()
![]() 分别于
分别于![]() 当
当![]() 为等腰三角形时,五边形
为等腰三角形时,五边形![]() 的周长为
的周长为![]() .其中正确结论的序号是_____________________.
.其中正确结论的序号是_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90,D为AB的中点,AE∥DC,CE∥DA.
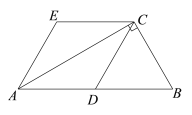
(1)求证:四边形ADCE是菱形;
(2)连接DE,若AC =![]() ,BC =2,求证:△ADE是等边三角形.
,BC =2,求证:△ADE是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是同-种蔬菜的两种裁植方法.甲:![]() 四珠顺次连结成为一个菱形,且
四珠顺次连结成为一个菱形,且![]() .乙:
.乙:![]() 四株连结成一个正方形。其中两行作物间的距离为行距;一行中相邻两株作物的距离为株距:设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积。设株距都为
四株连结成一个正方形。其中两行作物间的距离为行距;一行中相邻两株作物的距离为株距:设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积。设株距都为![]() ,其它客观因素都相同.则对于下列说法:
,其它客观因素都相同.则对于下列说法:
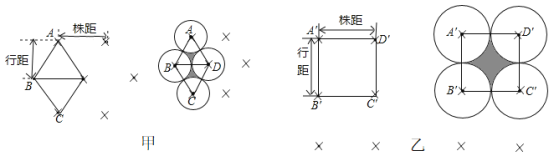
①甲的行距比乙的小;②甲的行距为![]() ;③甲、乙两种栽植方式,蔬菜形成的影子面积相同;④甲的空隙地面积比乙的空隙地面积少
;③甲、乙两种栽植方式,蔬菜形成的影子面积相同;④甲的空隙地面积比乙的空隙地面积少![]() .其中正确的个数为( )
.其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com