
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 、
、![]() 是弧
是弧![]() (异于
(异于![]() 、
、![]() )上两点,
)上两点,![]() 是弧
是弧![]() 上一动点,
上一动点,![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() .当点
.当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则
时,则![]() 、
、![]() 两点的运动路径长的比是( )
两点的运动路径长的比是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
连接BE,由题意可得点E是△ABC的内心,由此可得∠AEB=135°,为定值,确定出点E的运动轨迹是是弓形AB上的圆弧,此圆弧所在圆的圆心在AB的中垂线上,根据题意过圆心O作直径CD,则CD⊥AB,在CD的延长线上,作DF=DA,则可判定A、E、B、F四点共圆,继而得出DE=DA=DF,点D为弓形AB所在圆的圆心,设⊙O的半径为R,求出点C的运动路径长为![]() ,DA=
,DA=![]() R,进而求出点E的运动路径为弧AEB,弧长为
R,进而求出点E的运动路径为弧AEB,弧长为![]() ,即可求得答案.
,即可求得答案.
连结BE,
∵点E是∠ACB与∠CAB的交点,
∴点E是△ABC的内心,
∴BE平分∠ABC,
∵AB为直径,
∴∠ACB=90°,
∴∠AEB=180°-![]() (∠CAB+∠CBA)=135°,为定值,
(∠CAB+∠CBA)=135°,为定值,![]() ,
,
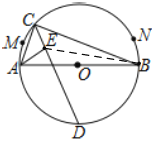
∴点E的轨迹是弓形AB上的圆弧,
∴此圆弧的圆心一定在弦AB的中垂线上,
∵![]() ,
,
∴AD=BD,
如下图,过圆心O作直径CD,则CD⊥AB,
∠BDO=∠ADO=45°,
在CD的延长线上,作DF=DA,
则∠AFB=45°,
即∠AFB+∠AEB=180°,
∴A、E、B、F四点共圆,
∴∠DAE=∠DEA=67.5°,
∴DE=DA=DF,
∴点D为弓形AB所在圆的圆心,
设⊙O的半径为R,
则点C的运动路径长为:![]() ,
,
DA=![]() R,
R,
点E的运动路径为弧AEB,弧长为:![]() ,
,
C、E两点的运动路径长比为: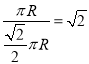 ,
,
故选A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明和小亮计划寒假结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在一个不透明的袋子中装有编号为![]() ,
,![]() ,
,![]() 的三个球(除编号外都完全相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和为偶数,则按照小明的想法参加敬老服务活动;若两次数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
的三个球(除编号外都完全相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和为偶数,则按照小明的想法参加敬老服务活动;若两次数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
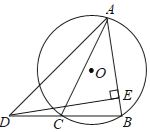
【题目】如图,⊙O中的弦BC等于⊙O的半径,延长BC到D,使BC=CD,点A为优弧BC上的一个动点,连接AD,AB,AC,过点D作DE⊥AB,交直线AB于点E,当点A在优弧BC上从点C运动到点B时,则DE+AC的值的变化情况是( )
A.不变B.先变大再变小C.先变小再变大D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着![]() 技术的发展,人们对各类
技术的发展,人们对各类![]() 产品的使用充满期待.某公司计划在某地区销售第一款
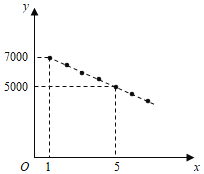
产品的使用充满期待.某公司计划在某地区销售第一款![]() 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第
产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第![]() (
(![]() 为正整数)个销售周期每台的销售价格为
为正整数)个销售周期每台的销售价格为![]() 元,
元,![]() 与
与![]() 之间满足如图所示的一次函数关系.
之间满足如图所示的一次函数关系.
(1)求![]() 与
与![]() 之间的关系式;
之间的关系式;
(2)设该产品在第![]() 个销售周期的销售数量为
个销售周期的销售数量为![]() (万台),
(万台),![]() 与
与![]() 的关系可用
的关系可用![]() 来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格上有一个△ABC,如果用(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,C点的顶点也在网格点上.
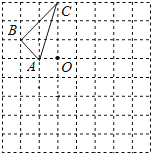
(1)作出△ABC关于点O的对称图形△A′B′C′(不写作法,但要在图中标出字母);
(2)写出A′、B′、C′三点的坐标;
(3)若网格上的最小正方形边长为1,求出△A′′BC′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 坐标为
坐标为![]() ,以
,以![]() 为直径作
为直径作![]() ,
,![]() 与抛物线交于
与抛物线交于![]() 轴上同一点
轴上同一点![]() ,连接
,连接![]() 、
、![]() .
.
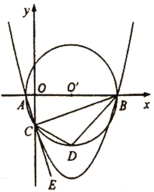
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)在(2)的条件下,抛物线上是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() 为
为![]() ,
,![]() 为
为![]() .
.
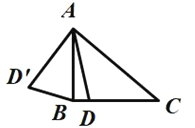
小明根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究,下面是小明的探究过程.请补充完整(说明:解答中所填数值均保留一位小数)
的变化而变化的规律进行了探究,下面是小明的探究过程.请补充完整(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 |
| 0.7 | 0.9 | 1.1 |
![]() 的值约为____________;
的值约为____________;
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图像.

(3)结合画出的函数图像,解决问题:
①线段![]() 的长度的最小值约为____________
的长度的最小值约为____________![]() ;
;
②![]() ,则
,则![]() 的长度
的长度![]() 的取值范围是____________.
的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在下列横线上:
每件销售利润____________________________;
销售量y(件)____________________________;
销售玩具获得利润w(元)____________________________;
(2)销售单价定为多少时,利润最大?
(3)若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com