
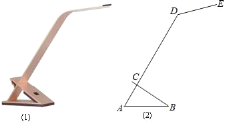
����Ŀ����ͼ��1����һ�ּ���̨�ƣ�����ṹͼ��2���е���Ϊ��ABC��BC������ֲ��ƣ���A��C��D��ͬһֱ���ϣ����á�ACB=90�㣬��A=60�㣬AB=16cm����ADE=135�㣬�Ƹ�CD��Ϊ40cm���ƹ�DE��Ϊ15cm��
��1����DE��ˮƽ���棨AB����ֱ�ߣ����ɵĽǣ�
��2����̨�Ƶĸߣ���E������ľ��룬�����ȷ��0.1cm����
���ο����ݣ�sin15��=0.26��cos15��=0.97��tan15��=0.27��sin30��=0.5��cos30��=0.87��tan30��=0.58����
���𰸡���1��15�㣻��2��45.5cm��
��������
��1��ֱ������ƽ���ߺʹ��߽����ó���EDF��ֵ��
��2������������Ǻ�����ϵ�ó�DN�Լ�EF��ֵ�������ó��𰸣�
��1����ͼ��ʾ������D��DF��AB������D��DN��AB�ڵ�N��EF��AB�ڵ�M��
������ɵã��ı���DNMF�Ǿ��Σ�
���NDF=90�㣬
�ߡ�A=60�㣬��AND=90�㣬
���ADN=30�㣬
���EDF=135�㩁90�㩁30��=15�㣬
��DE��ˮƽ���棨AB����ֱ�ߣ����ɵĽ�Ϊ15�㣻
��2����ͼ��ʾ���ߡ�ACB=90�㣬��A=60�㣬AB=16cm��
���ABC=30�㣬��AC=![]() AB=8cm��
AB=8cm��
�ߵƸ�CD��Ϊ40cm��
��AD=48cm��
��DN=ADsin60��=24![]() cm��
cm��
��FM=24![]() cm��
cm��
�ߵƹ�DE��Ϊ15cm��
��sin15��=![]() =
=![]() =0.26��
=0.26��
��ã�EF=3.9��
��̨�Ƶĸ�Ϊ��3.9+24![]() ��45.5��cm����
��45.5��cm����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
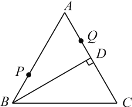
����Ŀ����ͼ,�ڡ�ABC��,PΪBC��һ��,PR��AB,����ΪR,PS��AC,����ΪS,��CAP=��APQ,PR=PS,����Ľ���:��AS=AR;��QP��AR;�ۡ�BRP�ա�CSP.������ȷ����(����)

A. �٢� B. �ڢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ���ֱ��س�����ֽƬ
���ֱ��س�����ֽƬ![]() ��������ֽƬ
��������ֽƬ![]() �ĶԽ���
�ĶԽ���![]() ��
��![]() ������ƴ����ͼ
������ƴ����ͼ![]() ��ʾ���ı���
��ʾ���ı���![]() �����м�հײ����ı���ǡ����������
�����м�հײ����ı���ǡ����������![]() �����ı���
�����ı���![]() �����Ϊ
�����Ϊ![]() ���������ε������( )
��������������( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��F��E��C��ͬһֱ���ϣ�AB��CD����ABE=��CDF��AF=CE��
��1����ͼ����������ȫ�������Σ�
��2���ӣ�1������ѡһ�����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
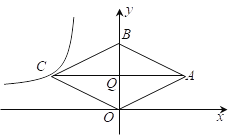
����Ŀ����ͼ������OABC�Ķ���O��ԭ�㣬����B��y���ϣ������Խ���AC��OB�ij��ֱ���6��4������������![]() ��ͼ����C.
��ͼ����C.
��1��д����A�����꣬����k��ֵ��
��2��������OABC��y������ƽ�ƶ��ٸ���λ���Ⱥ��A�����ڸ÷�����������ͼ���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У�
����֪��ʵ��a��b�����a��b����ôa2��b2����ͬλ����ȣ���ֱ��ƽ�У��������������ֱ�ǣ���ô����������ȣ��������ʽ![]() �����壬��ôx����
�����壬��ôx����![]() ����Щ���⼰�������ⶼ����������ǣ�������
����Щ���⼰�������ⶼ����������ǣ�������
A.�٢�B.�ۢ�C.�٢�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��߽�ˮ��ʶ,С�����ͳ�����Լ���7�����ˮ��,�������˵�3�����ˮ���,���õ������ݽ���������,���Ƴ���ͼ��ʾ��ͳ��ͼ.(��λ:��)
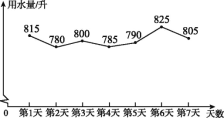
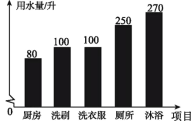
(1)����7����С���ÿ����ˮ����ƽ��������λ��;
(2)���3��С���ϴ�·���ˮռ��һ������ˮ���İٷֱ�;
(3)�������ͳ��ͼ�е���Ϣ,��С������һ��ȫ���Ľ�Լ��ˮ����,�����������Ľ����С���һ����(��30�����)�Ľ�Լ��ˮ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y��ax��b(a��0)��ͼ���뷴��������y��![]() (k��0)��ͼ���ڵڶ����������ڵ�A��B���㣬��y�ύ��C�㣬����A��AH��y�ᣬ����ΪH��OH��3��tan��AOH��
(k��0)��ͼ���ڵڶ����������ڵ�A��B���㣬��y�ύ��C�㣬����A��AH��y�ᣬ����ΪH��OH��3��tan��AOH��![]() ����B������Ϊ(m����2)��
����B������Ϊ(m����2)��
(1)���AHO���ܳ���
(2)��÷�����������һ�κ����Ľ���ʽ��

���𰸡�(1)��AHO���ܳ�Ϊ12��(2) �����������Ľ���ʽΪy��![]() ��һ�κ����Ľ���ʽΪy����
��һ�κ����Ľ���ʽΪy����![]() x��1.
x��1.
���������������: ��1���������к������ɵ�AH�ij������ݹ��ɶ������ɵ�AO�ij������������ε��ܳ����ɵô𰸣�
��2�����ݴ���ϵ�������ɵú�������ʽ��
�����������1����OH=3��tan��AOH=![]() ����
����
AH=4����A��-4��3����
�ɹ��ɶ�������
AO=![]() =5��
=5��
��AHO���ܳ�=AO+AH+OH=3+4+5=12��
��2����A���������y=![]() ��k��0������
��k��0������
k=-4��3=-12��
�����������Ľ���ʽΪy=![]() ��
��
��y=-2ʱ��-2=![]() �����x=6����B��6��-2����
�����x=6����B��6��-2����
��A��B���������y=ax+b����
![]() ��
��
��� ��
��
һ�κ����Ľ���ʽΪy=-![]() x+1��
x+1��
���㣺������������һ�κ����Ľ������⣮
�����͡������
��������
25
����Ŀ����ͼ����֪��A��C�ֱ��ڡ�GBE�ı�BG��BE�ϣ���AB=AC��AD��BE����GBE��ƽ������AD���ڵ�D������CD��
��֤����AB=AD��
��CDƽ�֡�ACE��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱߡ�![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() �ϵ�����������
�ϵ�����������![]() ����
����![]() ����һ����
����һ����![]() ʹ
ʹ![]() ��̣���
��̣���![]() ����СֵΪ_____
����СֵΪ_____![]() .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com