
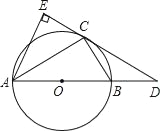
【题目】如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
(1)求证:DE是⊙O的切线;
(2)若AB=6,AE=![]() ,求BD和BC的长.
,求BD和BC的长.
【答案】(1)证明见解析;(2)BD=2;BC=![]() .
.
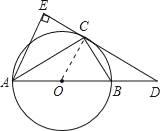
【解析】试题分析:(1)要证DE是⊙O的切线,只要连接OC,再证∠DCO=90°即可.
(2)已知两边长,求其它边的长,可以证明三角形相似,由相似三角形对应边成比例来求.
试题解析:解:(1)连接OC.∵AE⊥DC,∴∠E=90°.∵AC平分∠EAB,∴∠EAC=∠BAC.
又∵OA=OC,∴∠ACO=∠BAC,∴∠EAC=∠ACO,∴OC∥AE,∴∠OCD=∠E=90°,∴DC是⊙O的切线.
(2)∵∠D=∠D,∠E=∠OCD=90°,∴△DCO∽△DEA,∴ ![]() ,∴
,∴![]() ,∴
,∴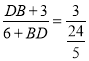 ,∴BD=2.∵AB是⊙O的直径,∴∠ACB=90°,∴∠E=∠ACB=90°.∵∠EAC=∠BAC,∴Rt△EAC∽Rt△CAB,∴
,∴BD=2.∵AB是⊙O的直径,∴∠ACB=90°,∴∠E=∠ACB=90°.∵∠EAC=∠BAC,∴Rt△EAC∽Rt△CAB,∴![]() ,∴
,∴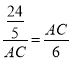 ,∴AC2=
,∴AC2=![]() .由勾股定理得:BC=
.由勾股定理得:BC=![]() =
=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某学校为了解本校八年级学生生物考试测试情况,随机抽取了本校八年级部分学生的生物测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如下统计图表.请你结合图表中所给信息解答下列问题:
等级 | 人数 |
A(优秀) | 40 |
B(良好) | 80 |
C(合格) | 70 |
D(不合格) |
(1)请将上面表格中缺少的数据补充完整;
(2)扇形统计图中“A”部分所对应的圆心角的度数是 ;
(3)该校八年级共有1200名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC的中点,F是线段CD上的动点.
(1)如图1,若CF=![]() CD,求证:ΔAEF是直角三角形;
CD,求证:ΔAEF是直角三角形;
(2)如图2,若点F与点D重合,点G在ED上,且AG=AD,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)有4张桌子,用第一种摆设方式,可以坐 人;用第二种摆设方式,可以坐 人;
(2)有n张桌子,用第一种摆设方式可以坐 人;用第二种摆设方式,可以坐 人(用含有n的代数式表示);
(3)一天中午,餐厅要接待120位顾客共同就餐,但餐厅中只有30张这样的长方形桌子可用,且每6张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,于点E

(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
符号、p分别表示一种运算,它对一些数的运算结果如下:
(0)=-1, (1)=0 , (2)=1 , (-3)=-4, (-4)=-5,……
p(-1)=-2,p(![]() )=1,p(
)=1,p(![]() )=
)=![]() , p(2)=4, p(-3)=-6,……
, p(2)=4, p(-3)=-6,……
根据以上运算规律,完成下列问题:
(1)计算:(-5)×p(![]() )+2
)+2
(2)已知x为有理数,且(x)+ p(![]() )=2×(-4),求x的值。
)=2×(-4),求x的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
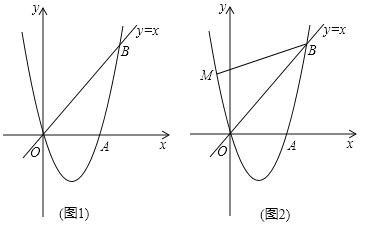
【题目】如图1,经过原点O的抛物线![]() (a≠0)与x轴交于另一点A(
(a≠0)与x轴交于另一点A(![]() ,0),在第一象限内与直线y=x交于点B(2,t).
,0),在第一象限内与直线y=x交于点B(2,t).
(1)求这条抛物线的表达式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小王某天下午营运是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6.
(1)将最后一名乘客送到目的地时,小王距下午出车时的出发点多远?
(2)若汽车耗油量为0.05升/千米,这天下午小王的汽车共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com