
 ��ͼ��������y=ax2+bx+4�������ύ��A��B��C���㣬ֱ��y=$\frac{4}{3}$x+4�������ύ��B��C�㣬���е�A��4��0����
��ͼ��������y=ax2+bx+4�������ύ��A��B��C���㣬ֱ��y=$\frac{4}{3}$x+4�������ύ��B��C�㣬���е�A��4��0�������� ��1�����������B�����꣬Ȼ�����ô���ϵ������������ߵĽ���ʽ���ɣ�
��2����CQ=e����������õ�CP=QC��=e������ֱ��$y=\frac{4}{3}x+4$����x=0ʱ��y=4����Rt��BCO�У�$CB=\sqrt{O{B^2}+C{O^2}}=5$������Q��QK��x�ᣬ����Ϊ��K�����У�QK��OB���õ���CKQ�ס�COB�����ǵõ�����ʽ$\frac{CQ}{CB}=\frac{CK}{CO}=\frac{KQ}{OB}$�����$CK=\frac{3}{5}e$��$KQ=\frac{4}{5}e$������C������C��H��x�ᣬ����Ϊ��H���õ�KH=QC��=e��C��H=KQ=$\frac{4}{5}$e�����ǵõ�$CH=CK+KH=\frac{3}{5}e+e=\frac{8}{5}e$�����C�䣨$\frac{8}{5}$e-3��$\frac{4}{5}$e�����������⣬��C��Ϊ�������ϵĵ㣬�õ�����$\frac{4}{5}e=-\frac{1}{3}��{��\frac{8}{5}e-3��^2}+\frac{1}{3}����\frac{8}{5}e-3��+4$�����${e_1}=\frac{55}{16}$�����ɵõ����ۣ�
��3�����������ĵ�M���������Σ���Ҫ�������ۣ���M��x��y�����ٵ�BM��BCʱ����ͼ2��ʾ���ɡ�ABO=45�㣬�õ���MBA+��CBO=45�㣬�ʵ�M��������������M1��M1E��y���ڵ�E����M1E=x��OE=-y�����BE=4-y������tan��M1BE=tan��BCO=$\frac{4}{3}$���õ�����$\frac{x}{4-y}$=$\frac{4}{3}$�����ֱ��BM1�Ľ���ʽΪy=-$\frac{3}{4}$x+4������y=-$\frac{3}{4}$x+4��y=-$\frac{1}{3}$x2+$\frac{1}{3}$x+4�����ɵõ�������ڵ�BM��BC����y��Գ�ʱ����ͼ3��ʾ���ɡ�ABO=��MBA+��MBO=45�㣬��MBO=��CBO�����ǵõ���MBA+��CBO=45�㣬�ʵ�M������������M2��M2E��y���ڵ�E����M2E=x��OE=y�����BE=4-y������tan��M2BE=tan��CBO=$\frac{3}{4}$���õ�����$\frac{x}{4-y}$=$\frac{3}{4}$���ֱ��BM2�Ľ���ʽΪ��y=-$\frac{4}{3}$x+4������y=-$\frac{4}{3}$x+4��y=-$\frac{1}{3}$x2+$\frac{1}{3}$x+4��-$\frac{4}{3}$x+4=-$\frac{1}{3}$x2+$\frac{1}{3}$x+4�����ɵõ������
��� �⣺��1����y=0ʱ����ֱ��$y=\frac{4}{3}x+4$�ã�$0=\frac{4}{3}x+4$����ã�x=-3��
���C��-3��0����
�֡�������y=ax2+bx+4������A��4��0����
������$\left\{\begin{array}{l}9a-3b+4=0\\ 16a+4b+4=0\end{array}\right.$��
��ã�$\left\{\begin{array}{l}a=-\frac{1}{3}\\ b=\frac{1}{3}\end{array}\right.$��
�������ߵĽ���ʽ�ǣ�$y=-\frac{1}{3}{x^2}+\frac{1}{3}x+4$��
��2����CQ=e����������⣬�ã�CP=QC��=e��
����ֱ��$y=\frac{4}{3}x+4$����x=0ʱ��y=4��
���B��0��4����OB=4��
�֡ߵ�C��-3��0����
��CO=3��
��Rt��BCO��$CB=\sqrt{O{B^2}+C{O^2}}=5$��
��ͼ1������Q��QK��x�ᣬ����Ϊ��K�����У�QK��OB��
���CKQ�ס�COB��
��$\frac{CQ}{CB}=\frac{CK}{CO}=\frac{KQ}{OB}$��
����$\frac{e}{5}=\frac{CK}{3}=\frac{KQ}{4}$��
��$CK=\frac{3}{5}e$��$KQ=\frac{4}{5}e$��
��ͼ1������C������C��H��x�ᣬ����Ϊ��H��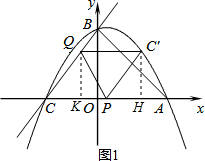
����KH=QC��=e��C��H=KQ=$\frac{4}{5}$e��
��$CH=CK+KH=\frac{3}{5}e+e=\frac{8}{5}e$��
�֡�CO=3��
��$OH=CH-CO=\frac{8}{5}e-3$��
��C�䣨$\frac{8}{5}$e-3��$\frac{4}{5}$e����
�������⣬��C��Ϊ�������ϵĵ㣬���У�$\frac{4}{5}e=-\frac{1}{3}��{��\frac{8}{5}e-3��^2}+\frac{1}{3}����\frac{8}{5}e-3��+4$��
��ã�${e_1}=\frac{55}{16}$��e2=0���������⣬��ȥ����
�൱$e=\frac{55}{16}$ʱ���У�$\frac{8}{5}e-3=\frac{8}{5}��\frac{55}{16}-3=2.5$��$\frac{4}{5}e=\frac{4}{5}��\frac{55}{16}=2.75$��
���C��������ǣ�2.5��2.75����
��3�����������ĵ�M�����꣬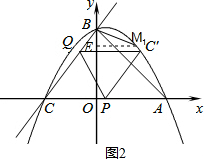 ��M��x��y����
��M��x��y����
�ٵ�BM��BCʱ����ͼ2��ʾ��
�ߡ�ABO=45�㣬
���MBA+��CBO=45�㣬�ʵ�M����������
����M1��M1E��y���ڵ�E����M1E=x��OE=-y��
��BE=4-y��
��tan��M1BE=tan��BCO=$\frac{4}{3}$��
��$\frac{x}{4-y}$=$\frac{4}{3}$��
��ֱ��BM1�Ľ���ʽΪ��y=-$\frac{3}{4}$x+4��
����y=-$\frac{3}{4}$x+4��y=-$\frac{1}{3}$x2+$\frac{1}{3}$x+4��
�ã�-$\frac{3}{4}$x+4=-$\frac{1}{3}$x2+$\frac{1}{3}$x+4��
��ã�x1=0��x2=$\frac{13}{4}$��
��y1=4��y2=$\frac{25}{16}$��
��M1��$\frac{13}{4}$��$\frac{25}{16}$����
�ڵ�BM��BC����y��Գ�ʱ����ͼ3��ʾ��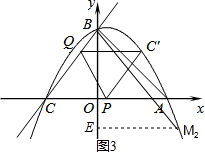
�ߡ�ABO=��MBA+��MBO=45�㣬��MBO=��CBO��
���MBA+��CBO=45�㣬
�ʵ�M����������
����M2��M2E��y���ڵ�E��
��M2E=x��OE=y��
��BE=4-y��
��tan��M2BE=tan��CBO=$\frac{3}{4}$��
��$\frac{x}{4-y}$=$\frac{3}{4}$
��ֱ��BM2�Ľ���ʽΪ��y=-$\frac{4}{3}$x+4��
����y=-$\frac{4}{3}$x+4��y=-$\frac{1}{3}$x2+$\frac{1}{3}$x+4�ã�-$\frac{4}{3}$x+4=-$\frac{1}{3}$x2+$\frac{1}{3}$x+4��
��ã�x1=0��x2=5��
��y1=4��y2=-$\frac{8}{3}$��
��M2��5��-$\frac{8}{3}$����
�������������������ĵ�M������Ϊ����$\frac{13}{4}$��$\frac{25}{16}$����5��-$\frac{8}{3}$����
���� ���⿼���˶��κ�����ͼ�������ʣ�����ϵ���������Ľ���ʽ����ֱ�������Σ�һ�κ��������ʣ��ⷽ�̵�֪ʶ�㣬��ȷ������ͼ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | 0 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
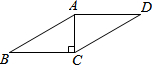 ��ͼ����?ABCD�У���A�����ߣ�����պ�Ϊ��C��AC=2����B=30�㣬��?ABCD���ܳ��ǣ�������
��ͼ����?ABCD�У���A�����ߣ�����պ�Ϊ��C��AC=2����B=30�㣬��?ABCD���ܳ��ǣ�������| A�� | $8+4\sqrt{3}$ | B�� | $4+2\sqrt{3}$ | C�� | 8 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x-x=3 | B�� | x2•x3=x5 | C�� | x6��x2=x3 | D�� | ��x2��3=x5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���x���꣩ | 2012 | 2013 | 2014 | �� |
| ��ѧ��ͯ����y���ˣ� | 2520 | 2330 | 2140 | �� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com