
【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
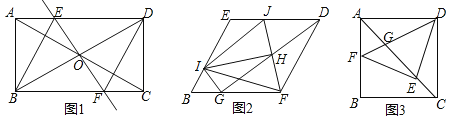
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
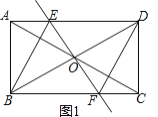
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
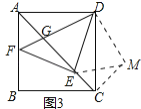
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.
【答案】(1)①证明见解析;②![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)①由![]() ,推出
,推出![]() ,
,![]() ,推出四边形
,推出四边形![]() 是平行四边形,再证明
是平行四边形,再证明![]() 即可.
即可.
②先证明![]() ,推出
,推出![]() ,延长即可解决问题.
,延长即可解决问题.
(2)![]() .只要证明
.只要证明![]() 是等边三角形即可.
是等边三角形即可.
(3)结论:![]() .如图3中,将
.如图3中,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,先证明
,先证明![]() ,再证明
,再证明![]() 是直角三角形即可解决问题.
是直角三角形即可解决问题.
(1)①证明:如图1中,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
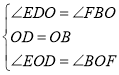 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是菱形.
是菱形.
②![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
(2)结论:![]() .
.
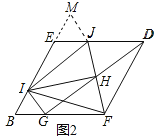
理由:如图2中,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() .
.
![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
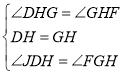 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]()
在![]() 和
和![]() 中,
中,
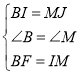 ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
(3)结论:![]() .
.
理由:如图3中,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
![]() ,
,
![]() 四点共圆,
四点共圆,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
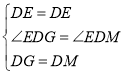 ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】矩形ABCO,O(0,0),C(0.3),A(a.0),(a≥3),以A为旋转中心顺时针旋转矩形ABCO,得到矩形AFED.
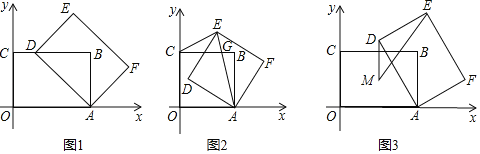
(1)如图1,当点D落在边BC上时,求BD的长;
(2)如图2,当a=3时,矩形AFEO的对角线A任交矩形ABCO的边BC于点G,连结CE.若△CGE是等腰三角形,求直线BE的解析式.
(3)如图3,当a=4时,矩形ABCD的对称中心为点M,△MED的面积为s,求s的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年西宁市高中招生体育考试测试管理系统的运行,将测试完进行换算统分改为计算机自动生成,现场公布成绩,降低了误差,提高了透明度,保证了公平.考前张老师为了解全市初三男生考试项目的选择情况(每人限选一项),对全市部分初三男生进行了调查,将调查结果分成五类:A、实心球(![]() kg);B、立定跳远;C、50米跑;D、半场运球;E、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
kg);B、立定跳远;C、50米跑;D、半场运球;E、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
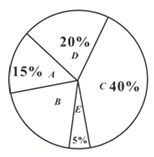
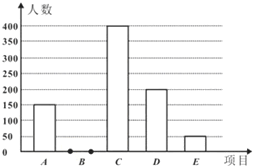
(1)将上面的条形统计图补充完整;
(2)假定全市初三毕业学生中有5500名男生,试估计全市初三男生中选50米跑的人数有多少人?
(3)甲、乙两名初三男生在上述选择率较高的三个项目:B、立定跳远;C、50米跑;D、半场运球中各选一项,同时选择半场运球、立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受地震的影响,某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从两养殖场调运鸡蛋到超市的路程和运费如表:
到超市的路程(千米) | 运费(元/斤千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
(1)若某天调运鸡蛋的总运费为2670元,则从甲、乙两养殖场各调运了多少斤鸡蛋?
(2)设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,E为AB的中点,P为BC上一动点,作PQ⊥EP交直线CD于点Q,设点P每秒以1个单位长度的速度从点B运动到点C停止,在此时间段内,点Q运动的平均速度为每秒_____个单位.
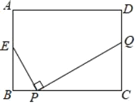
查看答案和解析>>
科目:初中数学 来源: 题型:
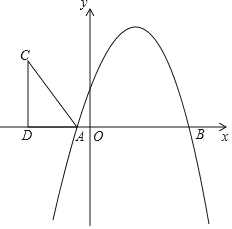
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直x轴于点D,连接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,如图转盘甲和乙,方式一:转动转盘甲,指针指向A区域时,所购物品享受9折优惠,指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向的区域字母相同,所购物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区域的可能性相同(若指针指向分界线,则重新转动转盘).
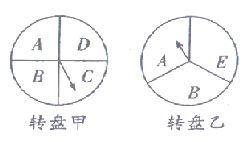
(1)若顾客选择方式一,求享受9折优惠的概率.
(2)若顾客选择方式二,请用列表法或树状图法列出所有可能出现的结果:并求顾客享受8折优惠的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com