
����Ŀ��ij�����ڶ�����ڼ俪չ�Żݻ���������߿���ͨ��ת��ת�̵ķ�ʽ�����ۿ��Żݣ����λ�������ַ�ʽ����ͼת�̼��ң���ʽһ��ת��ת�̼ף�ָ��ָ��A����ʱ��������Ʒ����9���Żݣ�ָ��ָ�������������Żݣ���ʽ����ͬʱת��ת�̼�ת���ң�������ת�̵�ָ��ָ���������ĸ��ͬ��������Ʒ����8���Żݣ�����������Ż�.��ÿ��ת���У�ָ��ָ��ÿ������Ŀ�������ͬ����ָ��ָ��ֽ��ߣ�������ת��ת�̣�.
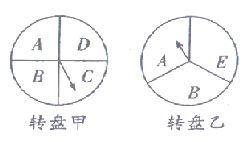
(1)���˿�ѡ��ʽһ��������9���Żݵĸ���.
(2)���˿�ѡ��ʽ���������б�������״ͼ���г����п��ܳ��ֵĽ��������˿�����8���Żݵĸ���.
���𰸡���1��![]() ����2����״ͼ��������
����2����״ͼ��������![]() .
.
��������
��1����ת��ת�̼������ֵȿ��ܽ��������ָ��ָ��A����ֻ��1����������ø��ʹ�ʽ����ɵã�
��2������״ͼ�ó����еȿ��ܽ��������ȷ��ָ��ָ��ÿ���������ĸ��ͬ�Ľ���������ø��ʹ�ʽ����ɵã�
�⣺��1�����˿�ѡ��ʽһ��ת��ת�̼�һ�ι������ֵȿ��ܽ��������ָ��ָ��A����ֻ��1�������
��P(����9���Ż�)��![]() ��
��
��2������״ͼ���£�
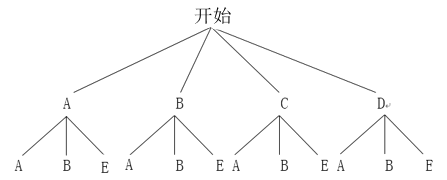
����״ͼ��֪����12�ֿ��ܳ��ֵĽ�������Ƿ����Ŀ�������ͬ.��������ָ��ָ��ͬһ����ĸ�����2�֣�
��P(����8���Ż�)��![]()


 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д� �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O������O��ֱ��EF��BD���ҽ�AC�ڵ�E����BC�ڵ�F������BE��DF����BEƽ�֡�ABD.
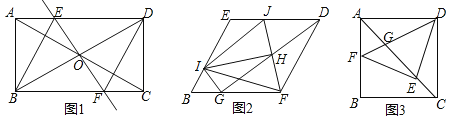
��1������֤���ı���BFDE�����Σ������EBF�Ķ�����
��2���ѣ�1��������BFDE���з����о�����ͼ2��G��I�ֱ���BF��BE���ϣ���BG=BI������GD��HΪGD���е㣬����FH�����ӳ�FH��ED�ڵ�J������IJ��IH��IF��IG����̽���߶�IH��FH֮�������������ϵ����˵�����ɣ�
��3���ѣ�1���о���ABCD�������⻯̽������ͼ3������ABCD����AB=ADʱ����E�ǶԽ���AC��һ�㣬����DE����EF��DE������Ϊ��E����AB�ڵ�F������DF����AC�ڵ�G����ֱ��д���߶�AG��GE��EC����֮�������������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������ABCD�Ķ���A������Ϊ(��1��1)����B��x���������ϣ���D�ڵ�������˫����y��![]() �ϣ�����C��CE��x�ύ˫�����ڵ�E������BE�����BCE�����Ϊ( )
�ϣ�����C��CE��x�ύ˫�����ڵ�E������BE�����BCE�����Ϊ( )
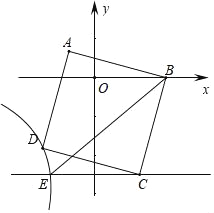
A. 5B. 6C. 7D. 8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
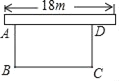
����Ŀ��Ϊ��Ӧ�����С�����ȫ���������С����٣�ij��λ������������������һ����οյ�������ɫֲ��������һ�߿�ǽ�������õ�ǽ��������18m������������36m����դ��Χ�ɣ������ABCD�յ��У���ֱ��ǽ�ı�AB��xm�����Ϊym2����ͼ����
��1����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2�������οյص����Ϊ160m2����x��ֵ��
��3�����õ�λ��8600Ԫ�����˼ס��ҡ���������ɫֲ�ﹲ400�ã�ÿ��ֲ��ĵ��ۺ�ÿ�����ֵĺ����õ�������±������ʱ���ֲ�������Թ�����ٿã���ʱ������ֲ�����ȫ�����ֵ����յ�������˵�����ɣ�
�� | �� | �� | |
���ۣ�Ԫ/�ã� | 14 | 16 | 28 |
�����õأ�m2/�ã� | 0.4 | 1 | 0.4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�ǵ���ֱ�������Σ���BAC��90�㣬AB��AC���ı���ADEF�������Σ���B��C�ֱ��ڱ�AD��AF�ϣ���ʱBD��CF��BD��CF������
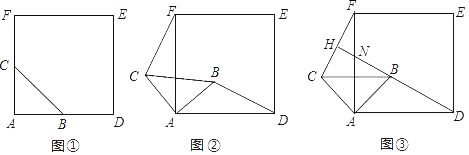
��1������ABC�Ƶ�A��ʱ����ת����0�㣼����90�㣩ʱ����ͼ����BD��CF����������������֤����������������˵�����ɣ�
��2������ABC�Ƶ�A��ʱ����ת45��ʱ����ͼ�����ӳ�DB��CF�ڵ�H��
��������֤��BD��CF��
��������AB��2��AD��3![]() ʱ�����߶�DH�ij���
ʱ�����߶�DH�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
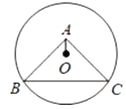
����Ŀ����ͼ��![]() ����B��C��Բ��O�ڵ���
����B��C��Բ��O�ڵ���![]() ���ڲ���
���ڲ���![]() ��
��![]() ��
��![]() ����
����![]() �İ뾶Ϊ�� ��
�İ뾶Ϊ�� ��
A.5B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ���B������Ϊ��1��0��
��1��������ABC����x��ԳƵ���A1B1C1��
��2����������ABC��ԭ��O����ʱ����ת90�����õ���A2B2C2��
��3����A1B1C1����A2B2C2����Գ�ͼ����������Գ�ͼ�Σ��������еĶԳ��
��4����A1B1C1����A2B2C2�����ĶԳ�ͼ�����������ĶԳ�ͼ�Σ�д�����еĶԳ����ĵ����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
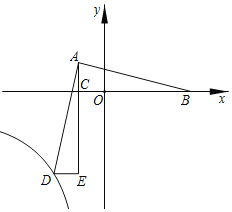
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC�Ķ���A��B������ֱ�Ϊ����1��1������3��0����ֱ�Ƕ���C��x���ϣ��ڡ�ADE�У���E��90�㣬��D�ڵ�������˫����y��![]() �ϣ��ұ�AE������C����AB��AD����BAD��90�㣬��k��ֵΪ��������
�ϣ��ұ�AE������C����AB��AD����BAD��90�㣬��k��ֵΪ��������
A.3B.4C.��6D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC�����Բ��AB����O��ֱ����DΪ��O��һ�㣬OD��AC������ΪE������BD.

(1)��֤��BDƽ����ABC��
(2) ����ODB=30��ʱ����֤��BC=OD.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com