
【题目】如图①,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
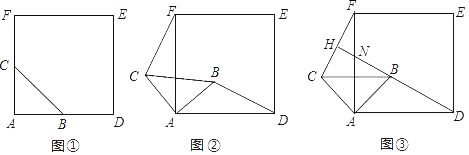
(1)当△ABC绕点A逆时针旋转α(0°<α<90°)时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H;
(ⅰ)求证:BD⊥CF;
(ⅱ)当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
【答案】(1)BD=CF,理由详见解析;(2)(ⅰ)详见解析;(ⅱ)![]() .
.
【解析】
(1)欲证明BD=CF,只要证明△CAF≌△BAD即可;
(2)(ⅰ)由(1)得△CAF≌△BAD,推出∠CFA=∠BDA,由∠FNH=∠DNA,∠DNA+∠NAD=90°,即可推出∠CFA+∠FNH=90°,由此即可解决问题;
(ⅱ)只要证明△DMB∽△DHF,可得![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
(1)BD=CF.
理由如下:由题意得,∠CAF=∠BAD=α,
在△CAF和△BAD中,
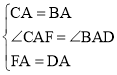 ,
,
∴△CAF≌△BAD,
∴BD=CF.
(2)(ⅰ)由(1)得△CAF≌△BAD,
∴∠CFA=∠BDA,
∵∠FNH=∠DNA,∠DNA+∠NAD=90°,
∴∠CFA+∠FNH=90°,
∴∠FHN=90°,即BD⊥CF.
(ⅱ)连接DF,延长AB交DF于M,

∵四边形ADEF是正方形,AD=3![]() ,AB=2,
,AB=2,
∴AM=DM=3,BM=AM﹣AB=1,
DB=![]()
∵∠MAD=∠MDA=45°,
∴∠AMD=90°,又∠DHF=90°,∠MDB=∠HDF,
∴△DMB∽△DHF,
![]() ,即
,即![]() ,
,
解得,DH=![]() .
.


科目:初中数学 来源: 题型:
【题目】2013年3月,某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象.已知A、B两点相距4米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米,参考数据:![]() )
)
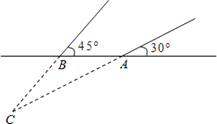
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是学习分式方程时,老师板书的问题和两名同学所列的方程

根据以上信息,解答下列问题
(1)冰冰同学所列方程中的x表示 ,庆庆同学所列方程中的y表示 ;
(2)两个方程中任选一个,并写出它的等量关系;
(3)解(2)中你所选择的方程,并回答老师提出的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,如图转盘甲和乙,方式一:转动转盘甲,指针指向A区域时,所购物品享受9折优惠,指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向的区域字母相同,所购物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区域的可能性相同(若指针指向分界线,则重新转动转盘).
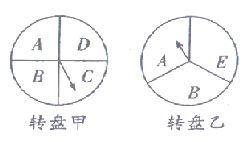
(1)若顾客选择方式一,求享受9折优惠的概率.
(2)若顾客选择方式二,请用列表法或树状图法列出所有可能出现的结果:并求顾客享受8折优惠的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
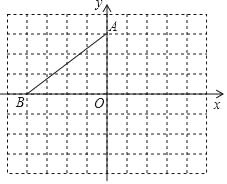
【题目】在平面直角坐标系中,点A、B的坐标分别是(0,3)、(﹣4,0),
(1)将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F,请在图中画出△AEF,并写出E、F的坐标;
(2)以O点为位似中心,将△AEF作位似变换且缩小为原来的![]() ,在网格内画出一个符合条件的△A1E1F1.
,在网格内画出一个符合条件的△A1E1F1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com