
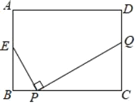
【题目】如图,矩形ABCD中,AB=6,BC=8,E为AB的中点,P为BC上一动点,作PQ⊥EP交直线CD于点Q,设点P每秒以1个单位长度的速度从点B运动到点C停止,在此时间段内,点Q运动的平均速度为每秒_____个单位.
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
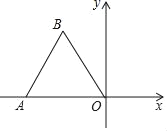
【题目】 如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
A.(1,![]() )B.(﹣1,2)C.(﹣1,
)B.(﹣1,2)C.(﹣1,![]() )D.(﹣1,
)D.(﹣1,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
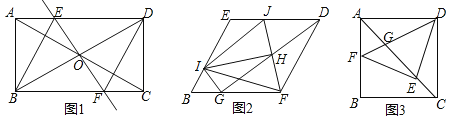
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名公务人员,对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如表所示:
应试者 | 面试 | 笔试 |
甲 | 86 | 90 |
乙 | 92 | 83 |
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为作为公务人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢后,用树状图表示或列表法求足球踢到了小华处的概率是多少
(2)如果从小明开始踢,经过踢三次后,球踢到了小明处的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
(1)第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少;若赚钱,赚多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com