
【题目】已知关于x的方程kx2﹣2(k+1)x+k﹣1=0有两个不相等的实数根.
(1)求k的取值范围.
(2)是否存在实数k,使此方程的两个实数根的倒数和等于1?若存在,求出k的值:若不存在,说明理由.
【答案】(1)k>﹣![]() 且k≠0;(2)不存在,理由见解析.
且k≠0;(2)不存在,理由见解析.
【解析】
(1)根据一元二次方程根的判别式、一元二次方程的定义,即可得到答案;
(2)根据一元二次方程根与系数的关系列出方程,解方程即可.
(1)∵方程kx2﹣2(k+1)x+k﹣1=0有两个不相等的实数根,
∴4(k+1)2﹣4k(k﹣1)>0,
即:12k+4>0,
解得,k>﹣![]() ,
,
又∵关于x的方程kx2﹣2(k+1)x+k﹣1=0是一元二次方程,
∴k≠0,
∴k>﹣![]() 且k≠0;
且k≠0;
(2)不存在,理由如下:
设关于x的方程kx2﹣2(k+1)x+k﹣1=0的两个根分别是:x1,x2.
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
假设:![]() ,即:
,即:![]() ,
,
解得:k=﹣3,
∵k>﹣![]() 且k≠0时,方程有两个不相等的实数根,
且k≠0时,方程有两个不相等的实数根,
∴不存在实数k,使此方程的两个实数根的倒数和等于1.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁):39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37 34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38 34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据,解答以下问题:
(1)小彬按“组距为5”列出了如下的频数分布表,每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图:
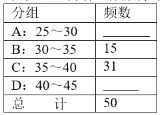
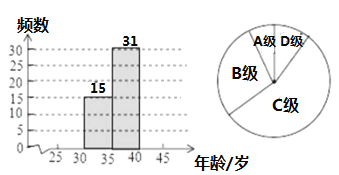
(2)在(1)的基础上,小彬又画出了如图所示的扇形统计图,图中B组所对的圆心角的度数为 ;
(3)根据(1)中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征.
查看答案和解析>>
科目:初中数学 来源: 题型:
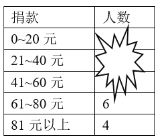
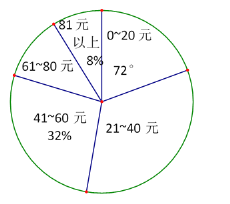
【题目】某校初三(1)班的同学踊跃为“雅安芦山地震”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但生活委员不小心把墨水滴在统计表上,部分数据看不清楚.
(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
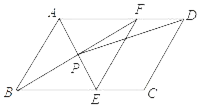
【题目】如图,ABCD中,点E,F分别是BC和AD边上的点,AE垂直平分BF,交BF于点P,连接EF,PD.
(1)求证:平行四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
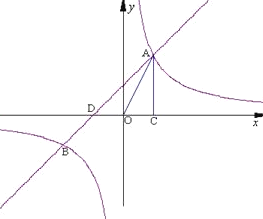
【题目】如图,已知反比例函数![]() (k1>0)与一次函数
(k1>0)与一次函数![]() 相交于A、B两点,AC⊥x轴于点C. 若△OAC的面积为1,且tan∠AOC=2 .
相交于A、B两点,AC⊥x轴于点C. 若△OAC的面积为1,且tan∠AOC=2 .
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
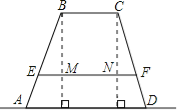
【题目】某高中学校为高一新生设计的学生板凳的正面视图如图所示,其中BA=CD,BC=20cm,BC、EF平行于地面AD且到地面AD的距离分别为40cm、8cm.为使板凳两腿底端A、D之间的距离为50cm,那么横梁EF应为多长?(材质及其厚度等暂忽略不计).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com