
【题目】正方形ABCD的边长为1,AB、AD上各有一点P、Q,如果![]() 的周长为2,求
的周长为2,求![]() 的度数.
的度数.
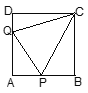
【答案】45°.
【解析】
首先从△APQ的周长入手求出PQ=DQ+BP,然后将△CDQ逆时针旋转90°,使得CD、CB重合,然后利用全等来解.
解:如图所示,
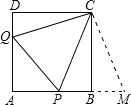
△APQ的周长为2,即AP+AQ+PQ=2①,
正方形ABCD的边长是1,即AQ+QD=1,AP+PB=1,
∴AP+AQ+QD+PB=2②,
①-②得,PQ-QD-PB=0,
∴PQ=PB+QD.
延长AB至M,使BM=DQ.连接CM,△CBM≌△CDQ(SAS),
∴∠BCM=∠DCQ,CM=CQ,
∵∠DCQ+∠QCB=90°,
∴∠BCM+∠QCB=90°,即∠QCM=90°,
PM=PB+BM=PB+DQ=PQ.
在△CPQ与△CPM中,
CP=CP,PQ=PM,CQ=CM,
∴△CPQ≌△CPM(SSS),
∴∠PCQ=∠PCM=![]() ∠QCM=45°.
∠QCM=45°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程kx2﹣2(k+1)x+k﹣1=0有两个不相等的实数根.
(1)求k的取值范围.
(2)是否存在实数k,使此方程的两个实数根的倒数和等于1?若存在,求出k的值:若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
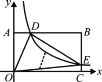
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
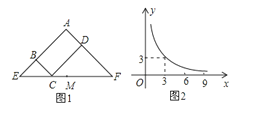
【题目】图(1)所示矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 满足的反比例函数关系如图(2)所示,等腰直角三角形
满足的反比例函数关系如图(2)所示,等腰直角三角形![]() 的斜边
的斜边![]() 过点
过点![]() ,
,![]() 为
为![]() 的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )
A. 当![]() 时,
时,![]()
B. 当![]() 时,
时,![]()
C. 当![]() 增大时,
增大时,![]() 的值增大
的值增大
D. 当![]() 增大时,
增大时,![]() 的值不变
的值不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18![]() m的地面上,若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是( )
m的地面上,若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是( )
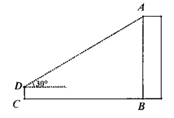
A.55.5mB.54mC.19.5mD.18m
查看答案和解析>>
科目:初中数学 来源: 题型:
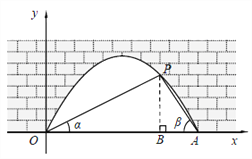
【题目】如图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
,以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
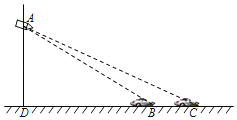
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=18°,∠ACD=14°.求电子警察安装在悬臂灯杆上的高度AD的长.
(参考数据:sin14°≈0.242,cos14°≈0.97,tan14°≈0.25,sin18°≈0.309,cos18°≈0.951,tan18°≈0.325)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中秋节”是我国的传统佳节,中秋赏月吃月饼.某蛋糕店销售“杏花楼”和“元祖”两个品牌的月饼,每个“杏花楼”月饼的售价是15元,每个“元祖”月饼的售价是12元.
(1)8月份,两个品牌的月饼一共销售180个,且总销售额不低于2460,则卖出“杏花楼”月饼至少多少个?
(2)9月份,月饼大量上市,受此影响,“杏花楼”月饼的售价降低了a%(a%<30%),销售量在八月份的最低销售量的基础上增加了5a个,“元祖”月饼的售价降低![]() a元,销售量在八份的最高销售量的基础上增加了
a元,销售量在八份的最高销售量的基础上增加了![]() a%,结果9月份的总销售额比8月最低销售额增加了1020元,求a的值.
a%,结果9月份的总销售额比8月最低销售额增加了1020元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
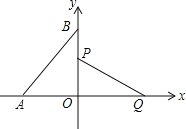
【题目】如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=![]() ,那么当点P运动一周时,点Q运动的总路程为__________.
,那么当点P运动一周时,点Q运动的总路程为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com